熟悉我的人都知道，我上大学前基本没有接触过编程，少有的几次也就是小学电脑课的scratch与小海龟和中学信息技术课的vb了。

然而当时接触的都只是基础语法，做一点在大学里几节课就能学会的东西。

所以，数据结构对于我来说是个全新的概念。我一直坚信：好记性不如烂笔头。只有写下来，才能促进我不断地回顾。

于是，这个系列诞生了…

我已经上了三周的课了，前几次老师讲了绪论、顺序表与链表。这些内容早在c和cpp课上被讲过多次，遂不再记录。

栈(Stack)

栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈，它是把新元素放到栈顶元素的上面，使之成为新的栈顶元素；从一个栈删除元素又称作出栈或退栈，它是把栈顶元素删除掉，使其相邻的元素成为新的栈顶元素。

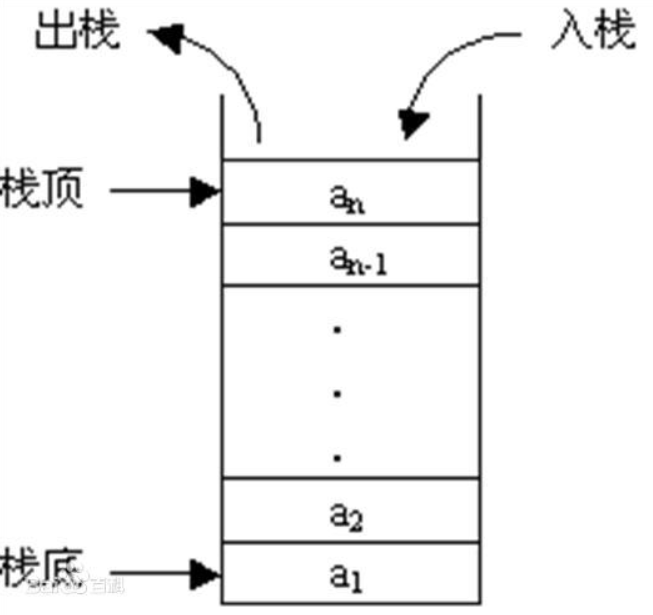
结合之前学过的知识，很容易想到用顺序表或链表来实现它。

栈的顺序表实现

容易想到，我们需要先创建一个顺序表。然而，这个表要多长呢？

如果设计得过长，会有空间的浪费；

如果设计得过短，加入新元素时难免会溢出。这时候就需要我们扩展这个表的长度，那问题又来了…要扩展多少呢？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
// 顺序栈
const int N = 10; //初始长度
const int dN = 5; //每次扩展增加的长度

template <class Type>
class Stack
{
    Type *stackBase; //栈底指针
    Type *stackTop;  //栈顶指针
    int stackSize;   //栈当前长度
public:
    Stack();           //初始化栈
    void push(Type e); //元素e入栈
    void pop();        //栈顶元素出栈
    bool empty();      //判断栈是否为空
    Type &top();        //返回栈顶元素
    int size();        //返回栈大小
};

template <class Type>
Stack<Type>::Stack()
{
    stackBase = (Type *)malloc(N * sizeof(Type));
    stackTop = stackBase;
    stackSize = N;
}
template <class Type>
void Stack<Type>::push(Type e)
{
    if (stackTop - stackBase >= stackSize) //栈溢出->扩展栈大小
    {
        stackBase = (Type *)realloc(stackBase, (stackSize + dN) * sizeof(Type));
        stackTop = stackBase + stackSize; //由于重新申请了空间,栈顶指针不能再指向原本空间的位置了,要在新的空间找到相对位置
        stackSize += dN;
    }
    *(stackTop++) = e; //元素入栈,栈顶指针+1
}
template <class Type>
void Stack<Type>::pop()
{
    if (stackTop != stackBase)
    {
        stackTop--; //出栈只需要让栈顶指针-1就可以了,数据完全可以放在那里不管,反正也没有影响
    }
}
template <class Type>
bool Stack<Type>::empty()
{
    return stackBase == stackTop; //若栈顶指针与栈底指针相同,说明栈为空
}
template <class Type>
Type &Stack<Type>::top()
{
    return *(stackTop - 1); //因为栈顶指针指向的实际上是空元素,所以要-1才是真正的栈顶元素
}
template <class Type>
int Stack<Type>::size()
{
    return stackSize;
}

可以看到，虽然我们可以正常地实现一个栈，但是初始大小和扩展大小的数值还是不好选取。

那有没有什么办法，可以让这个栈的大小更加灵活地变化呢？

是的，我们可以用链表。

栈的链表实现

众所周知，在链表头部插入和删除元素可以达到O(1)的速度。

很巧的是，对栈中元素的操作只需要在表的一端。这天造地设的一对，使得用链表来实现栈十分地容易。

首先来创建一个基础节点。

1
2
3
4
5
typedef struct stackNode
{
    Type data;              //数据域
    struct stackNode *next; //指针域
} stackNode, *LinkStack;

可以看到，用链表来实现栈十分简单，只需要一个简单的单向链表就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
// 链栈
template <class Type>
class Stack
{
    typedef struct stackNode
    {
        Type data;              //数据域
        struct stackNode *next; //指针域
    } stackNode, *LinkStack;
    LinkStack head = NULL;
    int stackSize = 0;

public:
    Stack();           //初始化栈
    void push(Type e); //元素e入栈
    void pop();        //栈顶元素出栈
    bool empty();      //判断栈是否为空
    Type &top();       //返回栈顶元素
    int size();        //返回栈大小
};
template <class Type>
Stack<Type>::Stack()
{
    head = (LinkStack)malloc(sizeof(stackNode));
    head->next = NULL;
}
template <class Type>
void Stack<Type>::push(Type e)
{
    LinkStack p = (LinkStack)malloc(sizeof(stackNode));
    p->data = e;
    p->next = head->next;
    head->next = p;
    stackSize++;
}
template <class Type>
void Stack<Type>::pop()
{
    LinkStack p = head->next;
    if (p != NULL)
    {
        head->next = p->next;
        free(p);
        stackSize--;
    }
}
template <class Type>
bool Stack<Type>::empty()
{
    return head->next == NULL;
}
template <class Type>
Type &Stack<Type>::top()
{

    return head->next->data;
}
template <class Type>
int Stack<Type>::size()
{
    return stackSize;
}

链表实现栈总体来说比较简单，就不具体地叙述了。

队列(queue)

队列与栈相反，是一种先进先出的数据结构。

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。

队列的顺序表实现与栈大体相同，只是要从表的前端取出，在此就不再赘述。

队列的链表实现

队列的基本操作有：

操作 简介
front() 返回队首元素的引用
back() 返回队尾元素的引用
push() 在队尾插入元素
pop() 从队首弹出元素
empty() 判断队列是否为空
size() 返回队列的大小

所以很显然，我们需要保存队列的队首和队尾指针。

队列的基本节点与栈基本类似：

1
2
3
4
5
typedef struct queueNode
{
    Type data;              //数据域
    struct queueNode *next; //指针域
} queueNode, *LinkQueue;

其余操作也与栈基本类似，只需借助链表的基本操作就可以了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
// 链队列
template <class Type>
class Queue
{
    typedef struct queueNode
    {
        Type data;              //数据域
        struct queueNode *next; //指针域
    } queueNode, *LinkQueue;

    LinkQueue queueFront = NULL; //队首指针
    LinkQueue queueBack = NULL;  //队尾指针
    int queueSize = 0;           //队列大小

public:
    Queue();
    Type &front();
    Type &back();
    void push(Type e);
    void pop();
    bool empty();
    int size();
};

template <class Type>
Queue<Type>::Queue()
{
    queueFront = (LinkQueue)malloc(sizeof(queueNode));
    queueFront->next = NULL;
    queueBack = queueFront;
}
template <class Type>
Type &Queue<Type>::front()
{
    return queueFront->next->data;
}
template <class Type>
Type &Queue<Type>::back()
{
    return queueBack->data;
}
template <class Type>
void Queue<Type>::push(Type e)
{
    LinkQueue p = (LinkQueue)malloc(sizeof(queueNode));
    p->data = e;
    p->next = NULL;
    queueBack->next = p;
    queueBack = p;
    queueSize++;
}
template <class Type>
void Queue<Type>::pop()
{
    if (queueSize)
    {
        LinkQueue p = queueFront->next;
        queueFront->next = p->next;
        free(p);
        queueSize--;
    }
}
template <class Type>
bool Queue<Type>::empty()
{
    return !queueSize;
}
template <class Type>
int Queue<Type>::size()
{
    return queueSize;
}

注意这里我们记录了队首指针和队尾指针，所以可以实现O(1)的push和pop。