数据结构算法笔记#1.2:栈的应用(1)

学完了栈和队列，现在我们来聊聊它们究竟有什么用。

这次我们来聊聊应用到栈的三种算法：括号匹配算法、走迷宫算法和算术表达式求值算法，由于第三者较为复杂，故下次再聊，本次先聊聊前两种算法。

括号匹配算法

问题描述

给出一段仅包含括号的表达式，要求不考虑嵌套顺序，判断表达式是否合法。

如：( [ { } ] ) 与 ( ) [ ] { [ ] } 都属于合法表达式；而 { ( } ) 以及 [ ( ] { 就属于非法表达式。

问题分析

面对这种问题，首先想到的是对每个字符依次处理：读到左括号，就可以先放着不管。只有当读到右括号时，才需分析是否有正确的左括号与之配对。

既然题目要求中不考虑嵌套，那我们只需考虑在该括号左边第一个未被处理的左括号是否与之配对就行。

例：读入" { ( [ "，接着再读入 ‘]’ ，就只需考虑 ‘[’ 是否与其匹配；再读入 ‘)’ ，由于 ‘[’ 已被处理，所以跳过不管，只需考虑 ‘(’ 即可。

对于程序来说，自然无法自己识别哪些被处理过哪些没被处理过。需要我们手动帮助它"识别"。这里我们很容易想到，已经处理过的括号不再有用，我们可以直接将其丢弃不管。

例：读入 “{ ( [” ，接着再读入 ‘]’ ，与 ‘[’ 匹配，匹配完后直接将 ‘[’ 丢弃，原序列变为"{ ("，此时再读入 ‘)’ ，就可以直接和最右端的 ‘(’ 进行匹配了。

显然，这个存储括号序列的结构只需要右端的压入和取出，也就是说我们可以用一个栈来实现。

代码实现

//括号匹配算法

#include <bits/stdc++.h>
using namespace std;

bool isBracketsMatch()
{
    stack<char> BRACKETS;
    char c = getchar(); //存储读入的数据
    while (c != '#')    //读到'#'说明读入结束
    {
        switch (c)
        {
        case '(':
        case '[':
        case '{':
            BRACKETS.push(c); //读到左括号:入栈
            c = getchar();
            break;
        case ')':
            if (BRACKETS.empty())
            {
                return false;
            }
            if (BRACKETS.top() == '(')
            {
                BRACKETS.pop();
                c = getchar();
                break;
            }
            else
            {
                return false;
            }
        case ']':
            if (BRACKETS.empty())
            {
                return false;
            }
            if (BRACKETS.top() == '[')
            {
                BRACKETS.pop();
                c = getchar();
                break;
            }
            else
            {
                return false;
            }
        case '}':
            if (BRACKETS.empty())
            {
                return false;
            }
            if (BRACKETS.top() == '{')
            {
                BRACKETS.pop();
                c = getchar();
                break;
            }
            else
            {
                return false;
            }
        default:
            return false;
        }
    }
    if (BRACKETS.empty())
        return true; //能运行到这里说明前面都没有错误
    return false;
}

int main()
{
    while (1)
    {
        cout << "请输入括号表达式,以'#'结尾:" << endl;
        cout << isBracketsMatch() << endl;
        fflush(stdin); //用来吞回车
    }
    return 0;
}

走迷宫算法

问题描述

给定一个迷宫和它的起点终点，设计一个算法找出从起点到终点的路径。

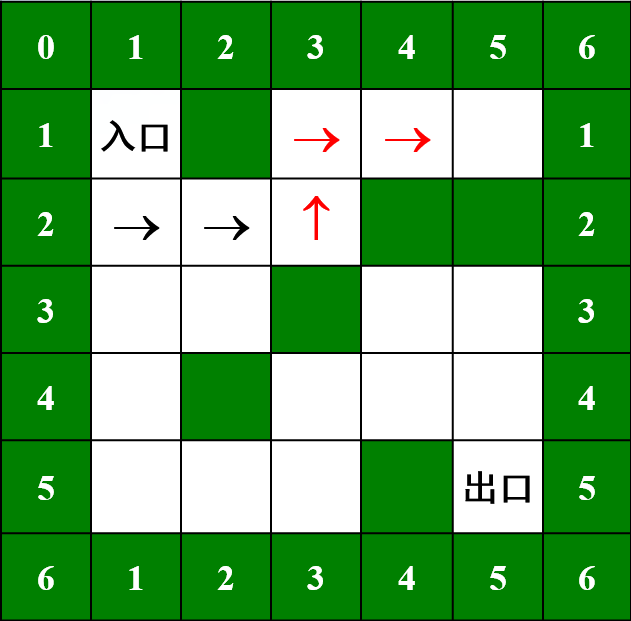
问题分析

程序没有人类那么聪明，能一眼看出哪些路能走哪些路不能走。所以我们要站在程序的角度上思考如何找到正确的路径。

那就先从一个方向开始走吧：按照"右上左下"的顺序，能往右就往右，否则就往上，以此类推。如图所示，走到(1,5)的位置会遇到死路。这时我们肯定会想着退回到上一个点：(1,4)：还是死路；(1,3)：还是死路…依次来到了(2,2)的位置，发现这个位置可以往下，便从这个位置继续开始寻路……

仔细观察这个过程，发现我们可以用栈来存储这些节点信息：

先分析当前节点A，如果有通路，就把该节点丢进栈里存起来。然后按一定顺序考虑它的通路(比如图里举例的"右上左下")。

先来看右边的通路，如果右边的通路没有其他通路了，我们就可以将这个节点丢弃，然后回退到前一个节点A。接着考虑上面的通路，以此类推…

如果右边通路的节点B还有其他通路，那我们就把节点B当作当前节点，执行相同的分析过程。

如果把节点A的四个方向都分析完了，那说明A是死路，只好将A删去，分析A节点的上一个节点。

不断循环这个过程，最后会出现两种情况：

1. 回到起点：那说明这个迷宫没有答案。
2. 走到终点：算法正确，输出结果。

可能听起来比较抽象，我们看代码吧：

代码实现

先来写一个最基本的节点单元，用于在栈中储存坐标。

typedef struct Pos
{
    int x, y;
    Pos(int cx, int cy)
    {
        x = cx;
        y = cy;
    }
} Pos;

然后构造迷宫和栈：

int MAZE[7][7] = { //迷宫数组, 1表示死路, 0表示通路
    {1, 1, 1, 1, 1, 1, 1},
    {1, 0, 1, 0, 0, 0, 1},
    {1, 0, 0, 0, 1, 1, 1},
    {1, 0, 0, 1, 0, 0, 1},
    {1, 0, 1, 0, 0, 0, 1},
    {1, 0, 0, 0, 1, 0, 1},
    {1, 1, 1, 1, 1, 1, 1}};
stack<Pos> path; //用来存放路径

接着分析当前节点四个方向是否有通路，如果为死路，则返回(-1,-1)。

Pos findPass(Pos currentPos)
{
    Pos nextPos(-1, -1); //初始化, 默认下一个节点为死路
    //依次寻找为0的点, 即为通路
    if (!MAZE[currentPos.x][currentPos.y + 1]) //右
    {
        nextPos.x = currentPos.x;
        nextPos.y = currentPos.y + 1;
    }
    else if (!MAZE[currentPos.x + 1][currentPos.y]) //下
    {
        nextPos.x = currentPos.x + 1;
        nextPos.y = currentPos.y;
    }
    else if (!MAZE[currentPos.x - 1][currentPos.y]) //上
    {
        nextPos.x = currentPos.x - 1;
        nextPos.y = currentPos.y;
    }
    else if (!MAZE[currentPos.x][currentPos.y - 1]) //左
    {
        nextPos.x = currentPos.x;
        nextPos.y = currentPos.y - 1;
    }
    return nextPos;
}

然后是迷宫的核心算法，模拟走迷宫的过程，大体分为四种情况：

1. 走到终点：直接退出函数，输出结果。
2. 找到通路：为了避免重复走，将该点标记为死路(走过)，然后分析下一个节点。
3. 没有通路：回退到上一个节点。
4. 回到起点：栈空，无解。

void mazePath()
{
    Pos currentPos(1, 1), nextPos(-1, -1); //把当前坐标置为起点
    while (true)
    {
        if (currentPos.x == 5 && currentPos.y == 5) //走到终点
        {
            path.push(currentPos);
            break;
        }
        nextPos = findPass(currentPos);
        if (nextPos.x != -1 && nextPos.y != -1) //都不为-1, 说明有通路
        {
            path.push(currentPos);
            MAZE[currentPos.x][currentPos.y] = -1; //为了避免重复走, 将其标记为走过
            currentPos = nextPos;
        }
        else //都没通路, 回退
        {
            MAZE[currentPos.x][currentPos.y] = -1;
            currentPos = path.top(); //将栈顶元素取出, 作为当前坐标接着遍历
            path.pop();
        }
        if (path.empty()) //无路可走
        {
            break;
        }
    }
}

具体的实现代码应该不难理解(如果这都难理解的话，那算术表达式求值算法估计如天书了2333)，下面附上完整代码供参考。

或许有错误，还望大家指正。

//走迷宫算法

#include <bits/stdc++.h>
using namespace std;

typedef struct Pos
{
    int x, y;
    Pos(int cx, int cy)
    {
        x = cx;
        y = cy;
    }
} Pos;
int MAZE[7][7] = { //迷宫数组, 1表示死路, 0表示通路
    {1, 1, 1, 1, 1, 1, 1},
    {1, 0, 1, 0, 0, 0, 1},
    {1, 0, 0, 0, 1, 1, 1},
    {1, 0, 0, 1, 0, 0, 1},
    {1, 0, 1, 0, 0, 0, 1},
    {1, 0, 0, 0, 1, 0, 1},
    {1, 1, 1, 1, 1, 1, 1}};
stack<Pos> path; //用来存放路径

void mazePath();              //主要函数
Pos findPass(Pos currentPos); //寻找一个节点的上下左右四个方位是否有路
void printPath();             //打印路径

int main()
{
    mazePath();
    printPath();
    return 0;
}

void mazePath()
{
    Pos currentPos(1, 1), nextPos(-1, -1); //把当前坐标置为起点
    while (true)
    {
        if (currentPos.x == 5 && currentPos.y == 5) //走到终点
        {
            path.push(currentPos);
            break;
        }
        nextPos = findPass(currentPos);
        if (nextPos.x != -1 && nextPos.y != -1) //都不为-1, 说明有通路
        {
            path.push(currentPos);
            MAZE[currentPos.x][currentPos.y] = -1; //为了避免重复走, 将其标记为走过
            currentPos = nextPos;
        }
        else //都没通路, 回退
        {
            MAZE[currentPos.x][currentPos.y] = -1;
            currentPos = path.top(); //将栈顶元素取出, 作为当前坐标接着遍历
            path.pop();
        }
        if (path.empty()) //无路可走
        {
            break;
        }
    }
}
Pos findPass(Pos currentPos)
{
    Pos nextPos(-1, -1); //初始化, 默认下一个节点为死路
    //依次寻找为0的点, 即为通路
    if (!MAZE[currentPos.x][currentPos.y + 1]) //右
    {
        nextPos.x = currentPos.x;
        nextPos.y = currentPos.y + 1;
    }
    else if (!MAZE[currentPos.x + 1][currentPos.y]) //下
    {
        nextPos.x = currentPos.x + 1;
        nextPos.y = currentPos.y;
    }
    else if (!MAZE[currentPos.x - 1][currentPos.y]) //上
    {
        nextPos.x = currentPos.x - 1;
        nextPos.y = currentPos.y;
    }
    else if (!MAZE[currentPos.x][currentPos.y - 1]) //左
    {
        nextPos.x = currentPos.x;
        nextPos.y = currentPos.y - 1;
    }
    return nextPos;
}
void printPath()
{
    int tempMaze[7][7];
    while (!path.empty())
    {
        Pos tempPos = path.top();
        tempMaze[tempPos.x][tempPos.y] = 1;
        path.pop();
    }
    for (int i = 0; i < 7; i++)
    {
        for (int j = 0; j < 7; j++)
        {
            if (tempMaze[i][j] == 1)
                cout << ' ';
            else
                cout << '#';
        }
        cout << endl;
    }
}