本来这个栏目是专门记录我的课堂笔记的，但我课余时间一不小心又接触了一些课外的算法，不记下来吧，就怕忘掉；记下来，又不知道该放在哪个栏目。

最后决定跟这个学期的课堂笔记放在一起，当作一个额外的番外篇。

就专门记录一些零零散散的小算法吧！

幂

求幂，是一个从刚开始接触编程就会学习的算法。在日常生活中也经常会用到。

然而，一开始我们只会接触到最基础的求幂算法：求x^n，便是进行n次循环，然后一次次乘以x。

1
2
3
4
5
6
7
int power(int x, int n)
{
    int ans = 1;
    for (int i = 0; i < n; i++)
        ans *= x;
    return ans;
}

这个算法，说起来好像没有一点问题。写起来简单，理解起来也简单，就是运行的时候有点低效……

为了不让我们的代码跑到猴年马月，我们引入了快速幂。

快速幂

设想一下，让你计算3^4，你会怎么算？

是3*3=9；9*3=27；27*3=81这样的一次次算……

还是3*3=9；9*9=81呢？

想必大多数人都是用后者吧。

既然知道了34=(32)*(32)，那我们只要计算一次32，再将其平方，就可以免去重复地计算两次3^2了。

至于32，那就计算(31)*(3^1)嘛。

如果用这个思想，是不是能减少很多运算次数呢？

当然，因为4是偶数，可以被我们拆分成2+2，但遇到奇数怎么办呢？

很简单，当n为奇数的时候，我们就把它拆分成(n-1)+1，(n-1)不就是偶数了嘛。

我们可以把这个过程写作一个递归式：

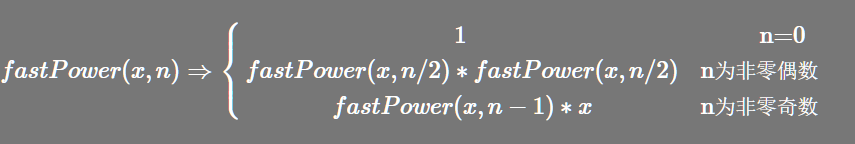
这样一来，我们的代码也就应运而生了。

递归形式

1
2
3
4
5
6
7
8
9
10
11
12
int fastPower(int x, int n)
{
    if (n == 0)
        return 1;
    if (n % 2)
        return fastPower(x, n - 1) * x;
    else
    {
        int temp = fastPower(x, n / 2);
        return temp * temp;
    }
}

然而，递归会造成许多空间的开销。但只要是递归能写出来的东西，便一定能用循环表示。

循环形式

1
2
3
4
5
6
7
8
9
10
11
12
int fastPower(int x, int n)
{
    int ans = 1;
    while (n)
    {
        if (n % 2)
            ans *= x;
        x *= x;
        n /= 2;
    }
    return ans;
}

这里用了点技巧：利用了C语言整数除法的特性。对于奇数n：n/2与(n-1)/2相等，所以，对于奇数，我们只要将其看作n-1，然后就行偶数的操作就行了，同时将答案提前乘上一个x，来弥补减掉的这个1。

对于偶数n，就类似递归形式的思路，先将n除以2，然后计算出x^2，再进行下一次循环。

最终形态

其实，如果要接着优化，还可以用上位运算，用n&1来判断奇偶性，用n>>=1来实现n除以2。

1
2
3
4
5
6
7
8
9
10
11
12
int fastPower(int x, int n)
{
    int ans = 1;
    while (n)
    {
        if (n & 1)
            ans *= x;
        x *= x;
        n >>= 1;
    }
    return ans;
}

至此，我们的幂运算效率已经非常高了，但有些时候（基本是算法题），我们需要对幂取模，所以这里我也给出取模的方法。

幂取模

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//非递归形式
int fastPower(int x, int n)
{
    int ans = 1;
    while (n)
    {
        if (n & 1)
            ans = ans * x % MOD;
        x = x * x % MOD;
        n >>= 1;
    }
    return ans;
}

//递归形式
int fastPower(int x, int n)
{
    if (n == 0)
        return 1;
    if (n % 2)
        return fastPower(x, n - 1) * x % MOD;
    else
    {
        int temp = fastPower(x, n / 2) % MOD;
        return temp * temp % MOD;
    }
}