数据结构算法笔记#2.1:二叉树的创建

结束了表结构的学习，我们终于迎来了二叉树。

这一次，我们从零开始，介绍一下树与二叉树的基本概念。

废话不多说，直接进入正题……

树

在聊二叉树之前，我们要先聊一聊树结构。

基本概念

树结构，顾名思义，就是像树一般拥有层级的结构。看一看左边的文章目录（手机端可能看不到），这就是一种树结构；家族的族谱也是一种树结构。构造树结构，能让数据更富有层次性，在一些后续的算法中，也会频繁地用到树，可以说，树是一种特别重要的数据结构。

基本名词

对于我们来说，树是一种全新的数据结构。所以有一些名词需要先了解一下。

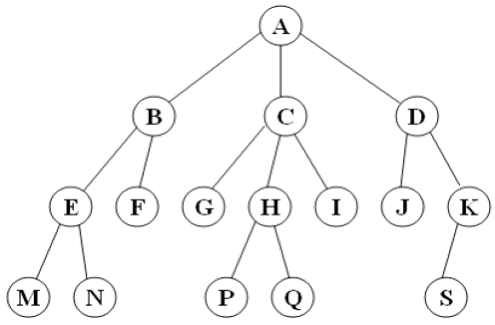
结点：树中的每一个元素。包含数据和指向其他结点的指针。
根结点：树中第一层的结点，图中为结点A。
子结点：某一结点的指针指向的结点。
父结点：指向某一结点的结点。
兄弟结点：与该结点拥有同一个父结点的结点。
结点的度：该结点拥有的子结点的个数。
叶结点：度=0的结点。
结点的层：根节点为第1层，第k层结点的子结点为k+1层。
树的深度(depth)：max(结点的层)

掌握了这些，我们就可以进入二叉树的学习了。

二叉树

二叉树，顾名思义，就是每个结点最多有两个子结点的树。换言之，每个结点的度都≤2。

一般来说，我们讲这两个结点分别称为左结点和右结点。

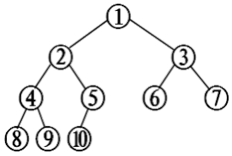
二叉树的表示

一般情况下，我们可以用两种方法来表示一棵二叉树：

二叉链表法

顾名思义，用有两个next指针的链表来表示二叉树，这样的储存结构十分直观：

struct Node
{
    char val;
    Node *left;
    Node *right;
}

然而，这种存储方式对于我们阅读来说，却是不太直观的。所以，我们引入了另一种方法：

字符串法

对于一棵树，我们也可以用字符串的嵌套结构来表示。

比如：对于图中这棵树，我们可以记为：1(2(4(8,9),5(10)),3(6,7))。

再比如：可以把另一棵树记为：A(B(C(E),D(,F)))，可以看到D的嵌套结构中，只有",F"的结构，说明没有左子树，只有值为F的右子树。

二叉树的构建

好了，说了这么多，我们也该开始构建我们的二叉树了。

为了再复习一遍二叉树的两种保存结构，我们就来实现一下用字符串表示法的树构造二叉链表树的过程吧。

思路分析

读入一串字符A(B(C(E),D(,F)))，毫无疑问，放在最前面的A肯定是赋给根节点，那后面的部分呢？

我们先举另外一个例子：对于(A,B)，我们肯定很容易看出，A是在左子结点，B在右子结点，但是要怎么设计算法区分呢？

可以发现，左右最大的区别，就是B的前面有逗号，而A的没有。所以就可以靠这个来区分左右了。

temp->val = c;
if (str[k - 1] == ',') //字母的前一位为逗号,说明在右树
    node->right = temp;
else
    node->left = temp;

当遇到不是字母的时候，我们就需要分类讨论：

首先是遇到左括号‘（’的情况：很显然可以直接跳过，不用去管，这时如果下一个字符也是符号（比如逗号），那就可以直接跳过两个字符，为了减少一次循环，我们可以直接跳过两个字符。

其次是遇到逗号‘，’的情况：显然，也可以直接跳过（好吧只要是标点符号都可以跳过），因为逗号后面有可能会出现右括号，所以我们也顺带判断一下是否是右括号，是的话直接一起跳过。

最后是右括号的情况，不用想，直接跳过。

代码实现

void BinaryTree::createNode(BTLink &node)
{
    node = (BTLink)malloc(sizeof(Node));
    if (node)
        node->left = node->right = NULL;
}

void BinaryTree::createTree(BTLink &node, string str)
{
    static int k = 1; //k用于指向字符串中各字符
    char c = str[k];
    while (c)
    {
        //当前字符为字母:存入树中
        if (c >= 'A' && c <= 'Z')
        {
            BTLink temp;
            createNode(temp);
            temp->val = c;

            if (str[k - 1] == ',') //字母的前一位为逗号,说明在右树
                node->right = temp;
            else
                node->left = temp;

            k++;
            createTree(temp, str); //从当前结点开始继续递归
        }
        else
        {
            if (c == '(') //当前为左括号
            {
                if (str[k + 1] == ',') //如果左括号的下一位是逗号,直接跳过两个字符
                    k += 2;
                else //如果不是,判断下一个字符
                    k++;
            }
            else if (c == ',') //当前为逗号
            {
                if (str[k + 1] == ')') //如果下一个字符为右括号,直接跳过这两个字符
                    k += 2;
                else //如果不是,说明下一个字符属于上一层的子结点,回溯
                {
                    k++;
                    return;
                }
            }
            else if (c == ')') //当前为右括号,回溯到上一层
            {
                k++;
                return;
            }
        }
        c = str[k];
    }
}

二叉树的输出

与构建二叉树相反，输出的过程就是将二叉链表转换为字符串形式。

这个过程比较简单，就不再赘述，直接上代码：

void BinaryTree::showTree(BTLink node)
{
    if (!node)
        return;
    cout << node->val;

    if (node->left) //有左结点,将左结点递归
    {
        cout << '(';
        showTree(node->left);
    }
    else
    {
        if (node->right) //无左结点有右节点,先把左括号输出了
            cout << '(';
        else
            return;
    }

    if (node->right) //有右结点,将右结点递归
    {
        cout << ',';
        showTree(node->right);
        cout << ')';
    }
    else //无右结点,先把右括号输出了
    {
        cout << ')';
        return;
    }
}

完整代码

最后献上完整代码：

//二叉树

#include <bits/stdc++.h>
using namespace std;

// A(B(C(E),D(,F)))

class BinaryTree
{
    typedef struct Node
    {
        char val;
        Node *left;
        Node *right;
    } Node, *BTLink;

    BTLink root;                               //根结点
    void createNode(BTLink &node);             //创建一个结点
    void createTree(BTLink &node, string str); //创建一棵树
    void showTree(BTLink node);                //输出函数的递归部分

public:
    BinaryTree(string str);
    void showTree(); //用字符串形式输出
};

int main()
{
    string str = "A(B(C(E),D(,F)))";
    BinaryTree bt(str);
    bt.showTree();
    return 0;
}

BinaryTree::BinaryTree(string str)
{
    createNode(root);
    root->val = str[0];    //第一个元素赋给根结点
    createTree(root, str); //从根结点开始递归赋值
}

void BinaryTree::createNode(BTLink &node)
{
    node = (BTLink)malloc(sizeof(Node));
    if (node)
        node->left = node->right = NULL;
}

void BinaryTree::createTree(BTLink &node, string str)
{
    static int k = 1; //k用于指向字符串中各字符
    char c = str[k];
    while (c)
    {
        //当前字符为字母:存入树中
        if (c >= 'A' && c <= 'Z')
        {
            BTLink temp;
            createNode(temp);
            temp->val = c;

            if (str[k - 1] == ',') //字母的前一位为逗号,说明在右树
                node->right = temp;
            else
                node->left = temp;

            k++;
            createTree(temp, str); //从当前结点开始继续递归
        }
        else
        {
            if (c == '(') //当前为左括号
            {
                if (str[k + 1] == ',') //如果左括号的下一位是逗号,直接跳过两个字符
                    k += 2;
                else //如果不是,判断下一个字符
                    k++;
            }
            else if (c == ',') //当前为逗号
            {
                if (str[k + 1] == ')') //如果下一个字符为右括号,直接跳过这两个字符
                    k += 2;
                else //如果不是,说明下一个字符属于上一层的子结点,回溯
                {
                    k++;
                    return;
                }
            }
            else if (c == ')') //当前为右括号,回溯到上一层
            {
                k++;
                return;
            }
        }
        c = str[k];
    }
}

void BinaryTree::showTree(BTLink node)
{
    if (!node)
        return;
    cout << node->val;

    if (node->left) //有左结点,将左结点递归
    {
        cout << '(';
        showTree(node->left);
    }
    else
    {
        if (node->right) //无左结点有右节点,先把左括号输出了
            cout << '(';
        else
            return;
    }

    if (node->right) //有右结点,将右结点递归
    {
        cout << ',';
        showTree(node->right);
        cout << ')';
    }
    else //无右结点,先把右括号输出了
    {
        cout << ')';
        return;
    }
}
void BinaryTree::showTree()
{
    showTree(root);
}