上一周我们已经实现了一棵自己的二叉树。

我们知道，对于我们学过的数据结构，不论链表或是矩阵，都有其独特的遍历方式，以方便我们在其中处理数据。

那二叉树有没有呢？当然有，而且有三种主要的遍历方式。

我们这次就来聊聊二叉树的前序遍历、中序遍历和后序遍历。

遍历

所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问 题。 遍历是二叉树上最重要的运算之一，是二叉树上进行其它运算之基础。

对于二叉树的每个结点元素，我们可以将其本身记为N（Node），左子树与右子树分别记为L与R。

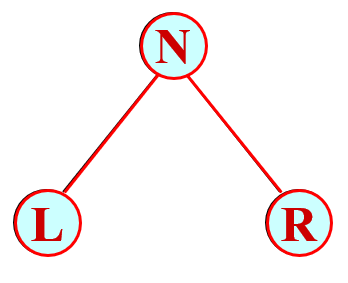
这样一来，对于每个结点我们就有六种遍历方式：NLR，LNR，LRN，NRL，RNL，RLN（其实就是对这三个字母的全排列）。我们可以将这六种分为三类：先遍历N的（NLR和NRL）、在中间遍历N的（LNR和RNL）与最后遍历N的（LRN和RLN），对于每类中的两种，其实只是L与R次序的问题，所以我们一般只考虑先L后R（反正反过来也是同样的原理）。

以上，我们便可以得出三种最典型的遍历方式：前序遍历(NLR) 、中序遍历(LNR) 与后序遍历(LRN) 。

递归形式

由于树结构的特殊性，大多数算法都是用递归实现最为方便，遍历也不例外。

前序遍历

算法分析

我们先从根结点开始，由于是NLR的遍历方式，所以先遍历它本身。

接着遍历L：如果有左子树，就对左子树调用前序遍历函数。

同理：如果有右子树，遍历R。

（这部分应该没什么理解难度吧……看看代码差不多了）

代码实现

1
2
3
4
5
6
7
8
9
10
11
void BinaryTree::preOrder(BTLink node)
{
    if (node)
    {
        cout << node->val << ' ';
        if (node->left)
            preOrder(node->left);
        if (node->right)
            preOrder(node->right);
    }
}

中序遍历

算法分析

其实三种遍历的递归算法都非常简单，仔细思考一下就会发现，本质上只是调换了遍历N的位置，后文便不一一赘述。

代码实现

1
2
3
4
5
6
7
8
9
10
11
void BinaryTree::midOrder(BTLink node)
{
    if (node)
    {
        if (node->left)
            midOrder(node->left);
        cout << node->val << ' ';
        if (node->right)
            midOrder(node->right);
    }
}

后序遍历

1
2
3
4
5
6
7
8
9
10
11
void BinaryTree::posOrder(BTLink node)
{
    if (node)
    {
        if (node->left)
            posOrder(node->left);
        if (node->right)
            posOrder(node->right);
        cout << node->val << ' ';
    }
}

非递归形式

虽然递归形式的遍历很容易写也很容易理解。但无奈考试很喜欢考非递归算法。

虽然非递归形式的遍历确实比起递归形式有些性能上的优势，但可读性和编写的容易度远远比不上递归形式。

其主要思路便是手动创建一个栈，来模拟递归时的操作，具体思路与递归算法大体相同，便不再细展开，直接看代码中的注释应该也不难理解。

前序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void BinaryTree::unRecPreOrder()
{
    stack<BTLink> tempStack;
    BTLink node = root;
    while (1)
    {
        //从左结点开始一路向下遍历,同时将途径的结点N遍历
        while (node)
        {
            cout << node->val << ' ';
            tempStack.push(node);
            node = node->left;
        }

        //无左子树,开始回退
        //回退值为空,说明遍历结束
        if (tempStack.empty())
            return;
        node = tempStack.top();
        tempStack.pop();

        //遍历当前结点的右子树
        node = node->right;
    }
}

中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void BinaryTree::unRecMidOrder()
{
    stack<BTLink> tempStack;
    BTLink node = root;
    while (1)
    {
        //从左边遍历到底
        while (node)
        {
            tempStack.push(node);
            node = node->left;
        }

        //无左子树,开始回退
        //回退值为空,说明遍历结束
        if (tempStack.empty())
            return;
        node = tempStack.top();
        tempStack.pop();

        //先输出N,然后遍历右子树
        cout << node->val << ' ';
        node = node->right;
    }
}

后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void BinaryTree::unRecPosOrder()
{
    stack<BTLink> tempStack;
    BTLink node = root;
    BTLink temp = NULL; //存放当前遍历过的结点
    while (1)
    {
        //从左边遍历到底
        while (node)
        {
            tempStack.push(node);
            node = node->left;
        }
        //栈空,说明遍历结束
        if (tempStack.empty())
            return;
        //栈顶结点无右子树,或右子树已被遍历过:将栈顶结点弹出并输出
        if (!tempStack.top()->right || tempStack.top()->right == temp)
        {
            temp = tempStack.top();
            tempStack.pop();
            cout << temp->val << ' ';
        }
        else //遍历右子树
            node = tempStack.top()->right;
    }
}

结

以上提到的三种遍历较为常见，当然还有其他不常见但有时也会用到的遍历方式，如层序遍历，不同于其他三种遍历方式，层序遍历是按每层的顺序进行遍历，用的也不是栈，而是队列。这里我也把层序遍历的代码放上来，有兴趣的朋友可以自行了解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void BinaryTree::levelOrder()
{
    queue<BTLink> tempQueue;
    tempQueue.push(root);
    while (!tempQueue.empty())
    {
        BTLink tempLink = tempQueue.front();
        cout << tempLink->val << ' ';
        tempQueue.pop();
        if (tempLink->left)
            tempQueue.push(tempLink->left);
        if (tempLink->right)
            tempQueue.push(tempLink->right);
    }
    cout << endl;
}