数据结构算法笔记#2.3:线索二叉树

我们之前已经接触过了二叉树的递归遍历和非递归遍历。

但是发现无论是哪种遍历方式，都离不开创建一个栈。

那么…有没有不需要栈的遍历方式？

当然有，只是比较麻烦——这次我们来聊聊线索二叉树。

引

我们知道，对于任何一棵二叉树，总是会有很多指向NULL的空指针域。经过简单的推理计算就可以得出：一棵拥有n个结点的二叉树，会有n+1个空指针域。

这些空指针域，白白放着也是浪费，为什么不把它们利用起来，让它们按照遍历次序指向下一个结点？

这样一来，对于各种不同的遍历方式，我们可以将空指针域指向不同的方向，从而构造出各种二叉树。一般来说，我们将左空指针指向当前结点的上一个结点（也称为前驱结点）；将右空指针指向当前结点的下一个结点（也称为后继结点）。我们将这些符合定义的树统称为线索二叉树（Threaded BinaryTree）。

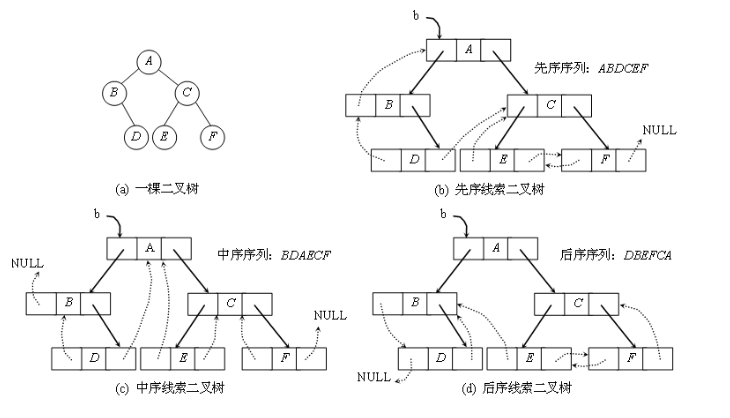
图片源于百度百科

线索二叉树

由于线索二叉树针对不同的遍历方式有不同的结构，我无法一一列举出来介绍，这次我就先介绍一下较为典型的中序线索二叉树。

中序线索二叉树

基本结点

虽然线索二叉树也是一棵二叉树，但它的结点结构还是与普通的二叉树有些许差别的。

想象一下，如果我们单纯的把空指针指向前驱或者后继，那在遍历的时候我们要怎么判断哪些是普通的指针，哪些又是前驱或后继指针呢？倘若不判断，顺着前驱指针回头又会重复遍历，岂不是会无限循环？

所以我们需要引入一个标识域来作为判断普通指针与前驱后继指针的标准。

对于左标识L-Flag：如果值为0，就说明是普通指针；如果值为1，就说明是前驱指针。
对于右标识R-Flag：如果值为0，就说明是普通指针；如果值为1，就说明是后继指针。

这样一来，我们的结点结构只要在普通二叉树的结点上稍作修改就可以得到了：

typedef struct Node
{
    char val;
    Node *left;
    Node *right;
    int lflag, rflag; //flag为0时为有子结点;左结点为1时指向前驱,右结点为1指向后继
} Node, *BTLink;

线索化

在线索化的过程中，我们需要将左空指针指向前驱结点，将右空指针指向后继结点。也就是说，需要同时对两个结点进行操作。那除了当前的结点，我们还需要额外记录一个结点。

一般情况下，我们选择记录前驱结点pre，若当前结点的左指针域为空，则将其指向前驱结点；同时，若前驱结点的右指针域为空，则将其指向当前结点。

这样一来，对单个结点与其前驱结点的线索化就完成了：

void BinaryTree::midThread(BTLink node, BTLink &pre)
{
    if (node && node->left)
        midThread(node->left, pre); //对左子树线索化

    if (!node->left) //左空指针域指向前驱
    {
        node->left = pre;
        node->lflag = 1;
    }
    if (pre && !pre->right) //前驱结点的右指针若为空:将当前结点作为前驱的后继
    {
        pre->right = node;
        pre->rflag = 1;
    }
    pre = node; //在对下一个结点线索化之前,将当前结点变成前驱
    
    if (node && node->right)
        midThread(node->right, pre); //对右子树线索化
}

对于整棵树而言，我们当然是要从根节点开始进行线索化。在处理完所有结点后，也别忘了将最后一次的前驱结点的右指针域指向NULL，保证后续的遍历能够正常退出。

//线索化
void BinaryTree::enMidThread()
{
    BTLink pre = NULL;
    midThread(root, pre); //从根结点开始线索化
    pre->right = NULL;    //处理最后一个结点
    pre->rflag = 1;
}

这样一来，线索化二叉树的基本算法都已经构建完成了，我们只需要在构造函数中调用enMidThread() 函数，就能将一棵普通的二叉树线索化了。

中序遍历

有了之前线索化的铺垫，再来进行中序遍历就十分容易了：

void BinaryTree::threadMidOrder()
{
    for (BTLink node = firstNode(root); node != NULL; node = nextNode(node))
        cout << node->val << ' ';
}

这里的firstNode() 是用来获取当前树按中序遍历的第一个结点，即为最左下角的那个结点；而nextNode() 是用来获取当前结点的下一个结点。其实完全不需要做成函数，可以分别展开。这里我用了函数主要是为了体现线索二叉树的特性：将复杂的树结构转换成简单的线性结构。

对于上述那两个函数，其实也十分容易理解，看代码就可以明白，就不多赘述：

BTLink firstNode(BTLink tree) //返回该树按中序遍历的第一个结点
{
    while (tree->lflag == 0)
        tree = tree->left;
    return tree;
}
BTLink nextNode(BTLink node) //返回该结点的下一个结点
{
    return node->rflag == 0 ? firstNode(node->right) : node->right;
}

至此，中序线索二叉树的所有结构都已经完成了，可以看到：在遍历的过程中没有用到任何一次栈或递归，但在构建的过程中还是需要递归。但是在需要频繁递归的情况下，线索二叉树还是有不小的优势的。

完整代码(包括二叉树创建)

//线索二叉树

#include <bits/stdc++.h>
using namespace std;

// A(B(C(E),D(,F)))

class BinaryTree
{
    typedef struct Node
    {
        char val;
        Node *left;
        Node *right;
        int lflag, rflag; //flag为0时为有子结点;左结点为1时指向前驱,右结点为1指向后继
    } Node, *BTLink;

    BTLink root;                               //根结点
    void createNode(BTLink &node);             //创建一个结点
    void createTree(BTLink &node, string str); //创建一棵树

    //线索化部分
    void enMidThread();                       //中序线索化
    void midThread(BTLink node, BTLink &pre); //中序线索化递归部分; node为当前结点,pre为前驱结点

    BTLink firstNode(BTLink tree) //返回该树按中序遍历的第一个结点
    {
        while (tree->lflag == 0)
            tree = tree->left;
        return tree;
    }
    BTLink nextNode(BTLink node) //返回该结点的下一个结点
    {
        return node->rflag == 0 ? firstNode(node->right) : node->right;
    }

public:
    BinaryTree(string str);
    void threadMidOrder(); //线索化中序遍历
};

int main()
{
    string str = "A(B(C(E),D(,F)))";
    BinaryTree bt(str);
    //bt.unRecMidOrder();
    bt.threadMidOrder();
    return 0;
}

BinaryTree::BinaryTree(string str)
{
    createNode(root);
    root->val = str[0];    //第一个元素赋给根结点
    createTree(root, str); //从根结点开始递归赋值
    enMidThread();         //中序线索化
}

void BinaryTree::createNode(BTLink &node)
{
    node = (BTLink)malloc(sizeof(Node));
    if (node)
    {
        node->left = node->right = NULL;
        node->lflag = node->rflag = 0;
    }
}

void BinaryTree::createTree(BTLink &node, string str)
{
    static int k = 1; //k用于指向字符串中各字符
    char c = str[k];
    while (c)
    {
        //当前字符为字母:存入树中
        if (c >= 'A' && c <= 'Z')
        {
            BTLink temp;
            createNode(temp);
            temp->val = c;

            if (str[k - 1] == ',') //字母的前一位为逗号,说明在右树
                node->right = temp;
            else
                node->left = temp;

            k++;
            createTree(temp, str); //从当前结点开始继续递归
        }
        else
        {
            if (c == '(') //当前为左括号
            {
                if (str[k + 1] == ',') //如果左括号的下一位是逗号,直接跳过两个字符
                    k += 2;
                else //如果不是,判断下一个字符
                    k++;
            }
            else if (c == ',') //当前为逗号
            {
                if (str[k + 1] == ')') //如果下一个字符为右括号,直接跳过这两个字符
                    k += 2;
                else //如果不是,说明下一个字符属于上一层的子结点,回溯
                {
                    k++;
                    return;
                }
            }
            else if (c == ')') //当前为右括号,回溯到上一层
            {
                k++;
                return;
            }
        }
        c = str[k];
    }
}

//线索化
void BinaryTree::enMidThread()
{
    BTLink pre = NULL;
    midThread(root, pre); //从根结点开始线索化
    pre->right = NULL;    //处理最后一个结点
    pre->rflag = 1;
}
void BinaryTree::midThread(BTLink node, BTLink &pre)
{
    if (node && node->left)
        midThread(node->left, pre); //对左子树线索化

    if (!node->left) //左空指针域指向前驱
    {
        node->left = pre;
        node->lflag = 1;
    }
    if (pre && !pre->right) //前驱结点的右指针若为空:将当前结点作为前驱的后继
    {
        pre->right = node;
        pre->rflag = 1;
    }
    pre = node; //在对下一个结点线索化之前,将当前结点变成前驱

    if (node && node->right)
        midThread(node->right, pre); //对右子树线索化
}

void BinaryTree::threadMidOrder()
{
    for (BTLink node = firstNode(root); node != NULL; node = nextNode(node))
        cout << node->val << ' ';
}