已知a和b是亲戚， b和c是亲戚，b和d也是亲戚。那c和d是不是亲戚呢……

要解决这种问题，看起来不是那么的容易。

没事，这次我们来聊一聊并查集，学完之后这种问题就能迎刃而解！

在介绍并查集之前，我要先介绍一种树的表示方法——树的双亲表示法。

双亲表示法

双亲表示法，实际上就是利用了树的每个结点只有一个父结点的特性来表示树。为了不引起歧义，我更喜欢称之为父亲表示法。

比如对于这样一棵二叉树：

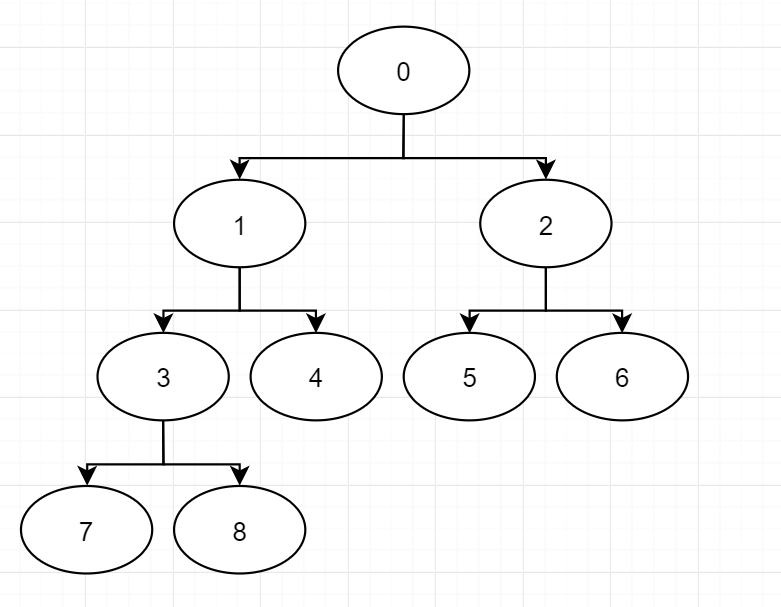
我们可以将其转化成线性结构，数组中的每一位代表一个结点，而其数据则代表其父结点的序号：

比如对于结点5，在数组tree中，tree[5]=2，则说明其父结点为2号结点。

用这种表示方式，很容易找到某个结点的父结点；然而缺点也很显然，如果要找结点的子结点，则需要遍历整个数组。

并查集

回到我们开头讲的那个问题，要判断两个人是不是亲戚，直接判断或许难度较高，但我们可以将他们的亲戚关系建立一棵树，在判断的时候只需要判断他们是否拥有同一个根结点即可，这样就大大简化了问题的难度。

我们建立起来的这种用双亲表示法表示的树形结构，由于只需实现合并与查找的功能，所以被称为并查集(union-find sets) 。

代码实现

初始化

在初始化并查集的时候，我们需要根据所需的元素个数n创建一个父结点数组，且由于其互相之间还没有关系，所以其父结点都指向自己。

1
2
3
4
5
6
vector<int> father(n);
void init(int n)
{
    for (int i = 0; i < n; i++)
        father[i] = i;
}

查找

查找的功能是找到某一个结点所在树的根结点（祖先），这便需要我们递归查找：

  • 如果该结点的父结点是自身，则说明已经找到。
  • 否则对其父结点继续递归查找。
1
2
3
4
int find(int x)
{
    return father[x] == x ? x : find(father[x]);
}

合并

合并的作用说白了就是建立两个结点之间的关系，可以直接将一个结点的父结点设为另一个，也可以分别找到它们的祖先，然后建立父子关系，我这里选择了后者。

1
2
3
4
void merge(int x, int y)
{
    father[find(x)] = find(y);
}

查找优化

之前学二叉树的时候已经知道，对于深度很深的树，递归查找的效率是非常低的，我们上文写的并查集也如此。作为一个本为了高效率而存在的数据结构，自然不允许出现效率这么低的情况。

于是，我们可以采用路径压缩的方法，在每次查找时将该结点的父结点设为根结点，这样一来，在下一次查找的时候就可以大大减少需要递归的次数，从而实现效率的提高。

1
2
3
4
int find(int x)
{
    return father[x] == x ? x : (father[x] = find(father[x]));
}

合并优化

看一下这两棵树，如果要将它们合并，是要将0的父结点设为9还是将9的父结点设为0呢？

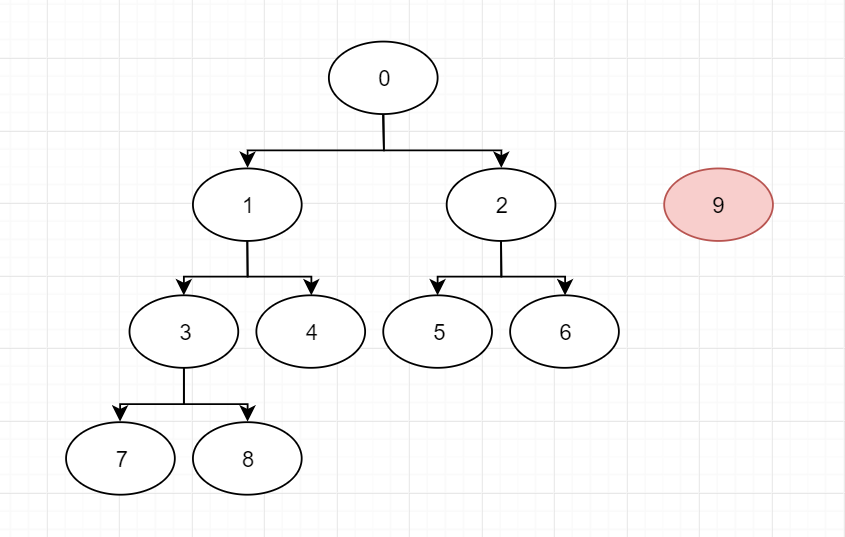
很显然，将9的父结点设为0较为合理，因为如果是将0的父结点设为9，那会使整棵树的深度增加，从而降低查找效率。

因此我们可以额外引入一个数组来记录每一个结点的深度，从而决定要如何合并。

1
2
3
4
5
6
7
8
9
10
vector<int> father(n);
vector<int> depth(n);
void init(int n)
{
    for (int i = 0; i < n; i++)
    {
        father[i] = i;
        depth[i] = 1;
    }
}

在初始化时先引入深度数组，并将其全部置为1。

1
2
3
4
5
6
7
void merge(int x, int y)
{
    int rx = find(x), ry = find(y);
    depth[rx] <= depth[ry] ? father[x] = y : father[y] = x; //将深度较大的结点设为深度较小的结点的父结点
    if (depth[rx] == depth[ry] && rx != ry)                 //深度相同但根不同:说明合并后深度要+1
        depth[ry]++;
}

结

容易发现，由于进行了查找优化，depth数组中储存的并不是真正的深度，而仅仅是起到参考的作用，但这并不会影响最终的结果。

并查集是一种十分优美的数据结构，在接下来图的学习中也会用到。在这里就作为一个铺垫，作为树结构的结尾，也翻开图结构的新一页。

这边顺便给出一段常用形式的板子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int fa[200005];
void init(int n)
{
    for (int i = 1; i <= n; i++)
        fa[i] = i;
}
int find(int x)
{
    return x == fa[x] ? x : (fa[x] = find(fa[x]));
}
void merge(int x, int y)
{
    fa[find(x)] = find(y);
}