结束了树的部分，我们终于迎来了图。

不论是在算法或是在离散数学中，图都是一种很重要的结构：后续的DFS、BFS以及最小生成树等重要算法都需要建立在图的基础上。

这是图的第一篇笔记，我们就先从图的概念以及邻接矩阵与邻接表入手。

一起走进图论的大坑（

基本概念

图，是一种邻接关系较为复杂的数据结构。不同于表的有规律，树的层级性，图看起来较为零散。

最基本的元素为顶点(Vertex) 与边(Edge) 。顶点，顾名思义，就是一个个存储数据的独立结点；而边，自然就是两个顶点之间的邻接关系。根据边的有向性，又可以将图分为无向图与有向图 。

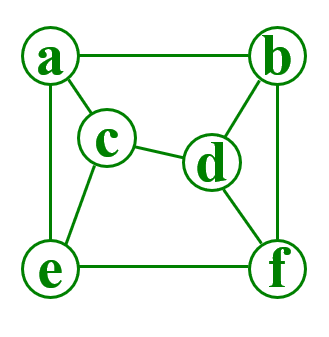
👆无向图

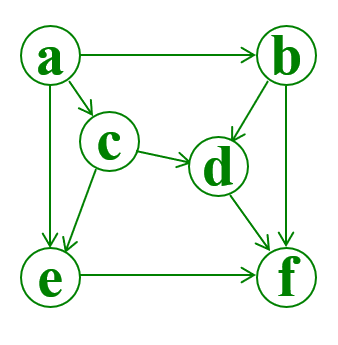
👆有向图

为了加以区分，一般将有向图的边称为弧(Arc) ，并将弧的起点终点分别称为"弧头"与"弧尾"。不过这些不太重要，平时大家还是都习惯称之为边。

对于每条边都有权值的图，也被称为网，或是带权图。但是为了方便，一般情况还是默认称为图，而对于不带权值的图，则默认将权值都视为1。

其他还有一些零星的概念，稍作了解，以后遇到的时候自然会明白：

  • 度（Degree） ：一个顶点的度是指与该顶点相关联的边的条数，顶点v的度记作d(v)，分为入度与出度。
  • 自环（Loop） ：若一条边的两个顶点为同一顶点，则此边称作自环。
  • 回路 ：若第一个顶点和最后一个顶点相同，则这条路径是一条回路。
  • 简单路径 ：若路径中顶点没有重复出现，则称这条路径为简单路径。
  • 路径长度 ：是指路径上边或弧的数目。
  • 连通图 ：在无向图中，如果从顶点vi到顶点vj有路径，则称vi和vj连通。如果图中任意两个顶点之间都连通，则称该图为连通图，否则，将其中的极大连通子图称为连通分量。

基本概念介绍完了，接下来我们聊聊在程序中如何表示一个图。

基本结构

对于一张图，我们所需要的基本数据无非就是顶点与边。对于顶点，直接用一个数组将其转换为数字即可。而对于边，我们需要记录其起点、终点以及权值(长度) 。一般来说，有两种记录方法，一种是邻接矩阵，另一种是邻接表 。

邻接矩阵应该比较好理解，如果有n个顶点，就创建一个n*n的矩阵，对于权值为w的边a->b，则将矩阵的[a][b]值置为w。而对于没有邻接关系的点，则将其值置为无穷。

但如果图较为稀疏（即稀疏图），用邻接矩阵会浪费过多的空间。回想一下当时处理稀疏矩阵时的做法，我们可以如法炮制，用三元组来储存。但三元组数组最大的缺点就是难以顺序遍历，不巧的是，图就偏偏需要顺序遍历（比如DFS等算法），所以我们不能用简单的三元组数组来保存。而应该用一种类似于三元组链表的结构，邻接表。

首先创建一个顶点数组，而顶点数组的每一个元素都指向一条链，这条链上的每一个结点对应的都是于其具有邻接关系的边。

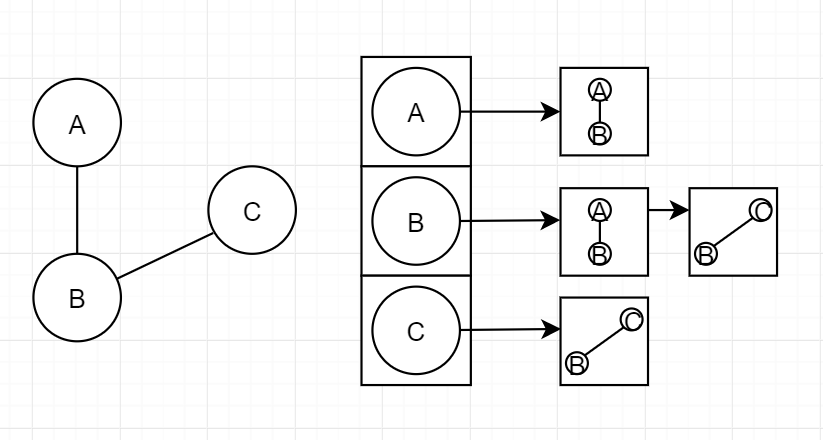
这样一来，两种基本结构我们都已经明白了，接下来就可以用代码进行实现了。

代码实现

邻接矩阵

首先定义一些基本数据，现在或许暂时用不到，但后续的很多算法都会用到：

1
2
3
4
int vertex_num = 0;           //顶点个数
int edge_num = 0;             //边数
vector<Type> vertexs;         //顶点信息
vector<vector<int>> adjacent; //邻接关系

这里的邻接矩阵可以用二维数组表示，我为了美观还是选择了二维的vector。

创建矩阵的方法很简单，传入一个顶点数组，一个邻接关系组，并将矩阵的对应坐标赋值即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
template <class T>
AdjacencyMatrix<T>::AdjacencyMatrix(vector<T> ver, vector<tuple<int, int, int>> adj)
{
    //数据初始化
    vertex_num = (int)ver.size();
    edge_num = (int)adj.size();
    vertexs = ver;
    visited.resize(vertex_num, 0);
    //初始化邻接关系
    vector<int> temp(vertex_num, INT_MAX);
    adjacent.resize(vertex_num, temp);
    for (auto i : adj)
    {
        adjacent[get<0>(i)][get<1>(i)] = get<2>(i);
        adjacent[get<1>(i)][get<0>(i)] = get<2>(i);
    }
}

这里默认是将图视为无向图，所以对应每条边都建立双向关系，如果是有向图只需删去

1
adjacent[get<1>(i)][get<0>(i)] = get<2>(i);

这句即可。

邻接表

相比起邻接矩阵，邻接表可能相对复杂。首先我们要构造出顶点数组，而顶点数组的每个元素除了顶点信息以外还需要一个指向第一条边的指针。

1
2
3
4
5
6
typedef struct VertexNode //顶点结点
{
    Type vertex;
    EdgeNode *firstEdge; //与其连接的第一条边
} VertexNode;
vector<VertexNode *> vertexs; //顶点数组

而对于边结点，起点、终点以及权值其实不需要全部记录，只需要记录终点与权值就够了，因为起点已经被指向它的顶点所确定了。

1
2
3
4
5
6
typedef struct EdgeNode //边结点
{
    int adjVex; //与其连接的顶点
    int weight; //权值
    EdgeNode *next;
} EdgeNode;

创建邻接关系的部分也与邻接矩阵大体相同，只不过写入邻接关系的部分需要稍作改动：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
template <class T>
AdjacencyList<T>::AdjacencyList(vector<T> ver, vector<tuple<int, int>> adj)
{
    //数据初始化
    vertex_num = (int)ver.size();
    edge_num = (int)adj.size();
    visited.resize(vertex_num, 0);
    //顶点数组赋值
    for (int i = 0; i < vertex_num; i++)
    {
        VertexNode *tempVer = (VertexNode *)malloc(sizeof(VertexNode));
        tempVer->vertex = ver[i];
        tempVer->firstEdge = NULL;
        vertexs.push_back(tempVer);
    }
    //邻接关系赋值
    for (auto i : adj)
    {
        addAdj(get<0>(i), get<1>(i), get<2>(i));
        addAdj(get<1>(i), get<0>(i), get<2>(i));
    }
}

addAdj()函数即是用前插法将数据结点插入顶点结点所确定的链中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
template <class T>
void AdjacencyList<T>::addAdj(int x, int y, int w)
{
    //创建一个临时结点
    EdgeNode *tempEdge = (EdgeNode *)malloc(sizeof(EdgeNode));
    tempEdge->adjVex = y;
    tempEdge->weight = z;
    tempEdge->next = NULL;

    //用前插法插入结点
    if (vertexs[x]->firstEdge == NULL)
        vertexs[x]->firstEdge = tempEdge;
    else
    {
        tempEdge->next = vertexs[x]->firstEdge;
        vertexs[x]->firstEdge = tempEdge;
    }
}

这样一来，构造邻接关系的部分就完成了。

结

作为图部分的第一篇笔记，其实并没有讲什么特别难的内容，更多地是对于图的抛砖引玉，先对图有个大体的了解，以便开始后面的学习。