数据结构算法笔记#3.2:图的遍历(DFS与BFS)

介绍完了图的基础知识，我们终于迎来图中最重要的一个知识点，也是许多算法都会用到的著名思想——DFS与BFS。

DFS即为深度优先搜索，BFS为广度优先搜索，他们就如同亲兄弟一般，处处相照应，前者需用到栈，而后者，则会用到队列。

它们都是图的遍历方法，执行一轮后即可以不同顺序遍历过图的所有顶点。

DFS(Depth-First-Search)

DFS的基本思想即为一条路走到黑 ，先顺着一条路搜索到底，然后再开始回溯，对之前没搜索过的岔路分别执行DFS。在这其中，已搜索过的顶点不会被重复搜索 。若DFS一轮后还有剩余顶点，则再对其进行DFS，当然，这种情况只出现于非连通图。

但看概念可能较为晦涩，我们来举个例子：

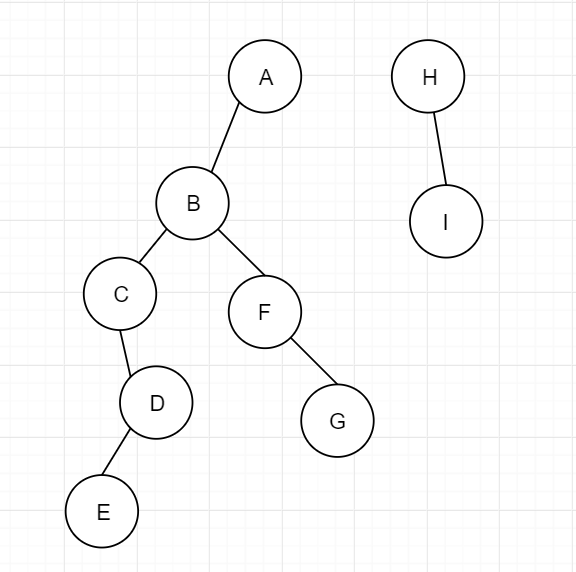
对于这张图，我们先从A开始DFS，先心无旁骛沿着一条路走到底：A->B->C->D->E 。当然，A->B->F->G也可以，在没有其他限定的情况下，遍历结果不具有唯一性 。我们假设使用的是前者，那么走到E后无路可走了，就进行回退。回退到D，但是与D相邻的C和E都已经搜索过，所以也无路可走，只好再次回退到B。这时发现有一个邻接点F还未被遍历过，便执行F->G的遍历。此时无路，开始回退过程，最终回到起点A，结束一轮搜索。但是H和I还未被遍历呀，没关系，我们就从H开始，执行H->I，最终遍历完成。

既然提到了**“回溯”** 。这个过程，那么很显然，DFS的代码需要用到栈（递归） 来实现。

图的前置框架已于上一篇笔记中给出，此处便不再赘述，仅指出一些关键变量：

template <class Type>
class AdjacencyMatrix
{
    int vertex_num = 0;           //顶点个数
    vector<Type> vertexs;         //顶点信息
    vector<vector<int>> adjacent; //邻接关系
    vector<int> visited;          //顶点是否被遍历过
};

可以看到，在原有的基础上，我们多添加了一个visited[]数组，这个数组的作用是记录每个顶点是否已被遍历过 ，若已遍历过，便不再重复遍历。

template <class T>
void AdjacencyMatrix<T>::DFS(int i)
{
    visited[i] = 1; //遍历过,做标记
    cout << vertexs[i] << "->";
    for (int j = 0; j < vertex_num; j++)
        if (adjacent[i][j] && !visited[j]) //对下一个没有遍历过的顶点DFS
            DFS(j);
}

这便是DFS的核心代码，利用递归的思想从一个顶点开始遍历，然后再对与其邻接的每个未遍历顶点进行递归遍历。直到遍历完所有连通顶点。但此时还会有非连通顶点未被遍历，于是需要对所有未遍历过的顶点都执行一次DFS。

template <class T>
void AdjacencyMatrix<T>::DFSTravel()
{
    for (auto &i : visited) //先把所有顶点设置为未遍历
        i = 0;
    for (int i = 0; i < vertex_num; i++) //对每个顶点进行DFS
        if (!visited[i])
            DFS(i);
    cout << "EXIT" << endl;
}

在程序中，只需要调用DFSTravel()函数即可。

BFS(Breadth-First-Search)

与深搜相对的，便是广搜。如果说深搜类似于“树的遍历”中的前序/中序/后序遍历，那么广搜就对应于树的层序遍历。与深搜的一条路走到黑不同，广搜的过程看起来较为“盲目”。基本思想是：先从一个顶点开始，遍历与其相邻的所有结点，再从这些节点开始，遍历与其相邻的所有结点（即为起点的二层邻接点），最终遍历完所有结点。就好比在北京城中，从最中心开始，先沿着一环走一圈，再沿着二环走一圈，然后是三环四环五环六环……这样的搜索过程看起来或许有些盲目，但它最终也是能不重复地遍历完所有顶点，且时间复杂度也与深搜并无二致。

由于搜索过程中需要先遍历所有邻接点，并将其邻接点储存起来进行下一轮遍历，所以程序实现过程中需要用到一个队列。

template <class T>
void AdjacencyMatrix<T>::BFSTravel()
{
    queue<int> tempQ;
    for (auto &i : visited) //先把所有顶点设置为未遍历
        i = 0;
    for (int i = 0; i < vertex_num; i++) //对每个顶点BFS
        if (!visited[i])
        {
            tempQ.push(i); //当前顶点入队
            while (!tempQ.empty())
            {
                i = tempQ.front();
                if (!visited[i]) //如果未访问过
                {
                    visited[i] = 1; //遍历过,做标记
                    cout << vertexs[i] << "->";
                }
                tempQ.pop();
                for (int j = 0; j < vertex_num; j++)
                    if (adjacent[i][j] && !visited[j]) //如果存在未遍历过的邻接顶点,入队
                        tempQ.push(j);
            }
        }
    cout << "EXIT" << endl;
}