数据结构算法笔记#3.3:最小生成树

一个有 n 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 n 个结点，并且有保持图连通的最少的边。

换句话说，一棵生成树就是有n-1条边的连通子图。而最小生成树(MST)，就是符合条件的子图中总权值最小的图。

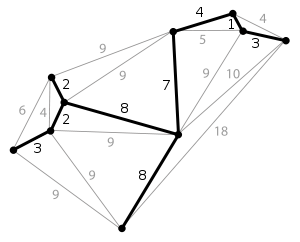
最小生成树在生活中的应用十分广泛，比如说在城市之间搭建通信网络，那最小生成树就能求出电缆长度最短的解法（当然，只是一个举例，现实生活中肯定还要考虑很多因素）。

最小生成树有两种构造方法，分别为“加点法”Prim算法与“加边法”Kruskal算法。

Prim

算法简介

Prim算法的基本思想是“加点”，大体思路就是将顶点们分为两个集合，集合X{}为当前选中的点，集合Y{}为未选中的点。初始情况下X{}为空，而Y{}包含所有顶点。

刚开始先选择一个顶点u作为起点加入X{}。然后从Y{}中寻找距离u最近的点v，将其加入X{}。此时的X{u,v}中就有了两个顶点。接下来从Y{}中继续寻找顶点距离u或v最近的顶点w，将其加入X{}。不断循环以上过程，直到X{}中有所有顶点，而Y{}为空。此时由以上选中的邻接关系组成的子图即为最小生成树。

老规矩，我们来举个例子：

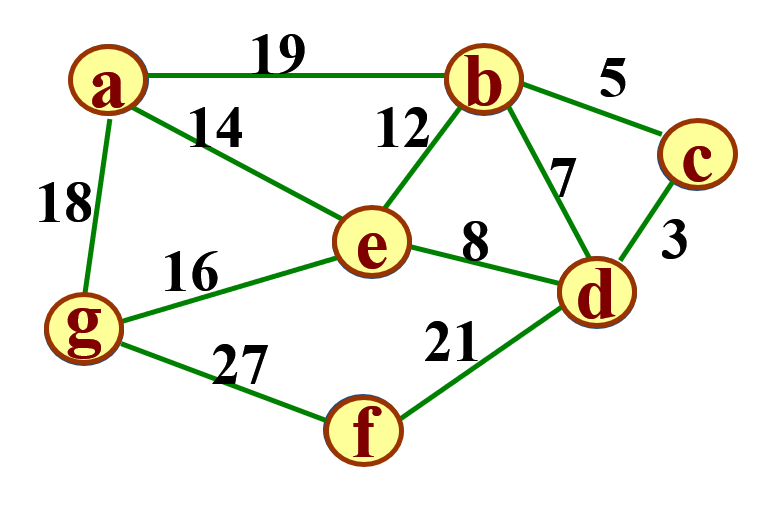
假设以b点作为起点。此时有 <b,a> <b,c> <b,d> <b,e> 四条边可以选，我们选择最短的 <b,c>=5，记录下来，并将c加入X{}集合。

接下来进行第二轮查找：由于X={b,c}，此时有 <b,a> <b,d> <b,e> <c,d> 可以选择，显然：<c,d>=3为最短边，所以选择d加入集合。

第三轮，因为<d,e>=8，所以加入e。第四轮，<e,a>=14。然后是第五轮选择g，第六轮选择f。此时所有顶点都被选择完毕，最小生成树也构造完毕了。

最小生成树即由上述选择的边构成：{<b,c> <c,d> <d,e> <e,a> <e,g> <d,f>}。

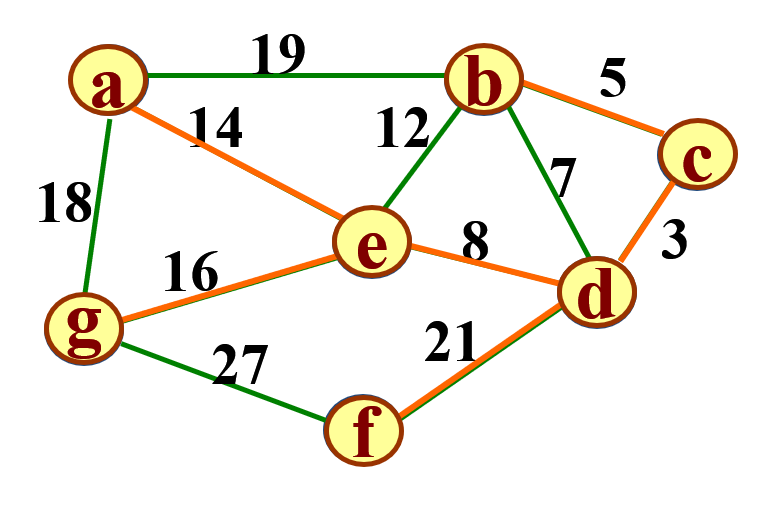
在Prim算法中，我们运用了“贪心”的思想。

代码实现

首先定义几个变量：

/*定义变量*/
vector<int> lowCost(vertex_num);     //记录当前点到剩余点的最小权值,-1为已遍历的标记
vector<int> mst(vertex_num);         //记录MST的邻接关系
int cost = 0;                        //整棵树的总权值
int curVex = -1;                     //当前顶点
int minCost = INT_MAX;               //记录最小权值

lowCost[]用来记录X{}到Y{}中剩余点的最小权值，同时用来记录已选择的点，将其置为-1；

mst[]记录邻接关系，最小生成树可以看作每个顶点有且只有唯一指向顶点的图，所以可以直接用一维数组来储存。

由于第一轮是先从起点u开始遍历，所以将lowCost[]中所有值都置为u到其的距离，并将u标记为-1：

for (int i = 0; i < vertex_num; i++) //从第u个点开始搜索,权值都为到u的权值
{
    lowCost[i] = adjacent[u][i];
    mst[i] = u;
}
lowCost[u] = -1;

接下来对剩余的n-1个点进行搜索，每次选择距离X{}中顶点最近的点，在选择完之后对lowCost[]数组中的数据进行更新，判断当前选择的点到Y{}中顶点是否有更近的路径，如果有，就将其更新：

for (int i = 1; i < vertex_num; i++) //对剩余点搜索
{
    minCost = INT_MAX;
    curVex = -1;
    for (int j = 0; j < vertex_num; j++) //找到到当前点权值最小的点
        if (lowCost[j] < minCost && lowCost[j] != -1)
        {
            minCost = lowCost[j];
            curVex = j;
        }
    cost += minCost;
    cout << vertexs[mst[curVex]] << "->" << vertexs[curVex] << ':' << minCost << endl;
    lowCost[curVex] = -1; //当前点标记已搜索
    for (int j = 0; j < vertex_num; j++)
        if (adjacent[curVex][j] < lowCost[j])
        {
            lowCost[j] = adjacent[curVex][j];
            mst[j] = curVex; //更新了权值,将其作为当前点继续搜索
        }
}

完整代码

int AdjacencyMatrix::prim(int u)
{
    /*定义变量*/
    vector<int> lowCost(vertex_num);     //记录当前点到剩余点的最小权值,-1为已遍历的标记
    vector<int> mst(vertex_num);         //记录MST的邻接关系
    int cost = 0;                        //整棵树的总权值
    int curVex = -1;                     //当前顶点
    int minCost = INT_MAX;               //记录最小权值
    for (int i = 0; i < vertex_num; i++) //从第u个点开始搜索,权值都为到u的权值
    {
        lowCost[i] = adjacent[u][i];
        mst[i] = u;
    }
    lowCost[u] = -1;
    for (int i = 1; i < vertex_num; i++) //对剩余点搜索
    {
        minCost = INT_MAX;
        curVex = -1;
        for (int j = 0; j < vertex_num; j++) //找到到当前点权值最小的点
            if (lowCost[j] < minCost && lowCost[j] != -1)
            {
                minCost = lowCost[j];
                curVex = j;
            }
        cost += minCost;
        cout << vertexs[mst[curVex]] << "->" << vertexs[curVex] << ':' << minCost << endl;
        lowCost[curVex] = -1; //当前点标记已搜索
        for (int j = 0; j < vertex_num; j++)
            if (adjacent[curVex][j] < lowCost[j])
            {
                lowCost[j] = adjacent[curVex][j];
                mst[j] = curVex; //更新了权值,将其作为当前点继续搜索
            }
    }
    return cost;
}

Kruskal

算法简介

与Prim算法所对应，Kruskal算法用的是“加边”的思想。既然最小生成树是需要所选边的权值最小，那就从整张图中权值最小的边开始选，直到选出连通图为止。看起来很简单，但在这其中有几个细节需要注意：首先是避免选出环 ，想象一下，要对 a,b,c 三点构造MST，如果已经选了 <a,b> <b,c> 那还能选择 <a,c> 吗？很显然是不行的，选择了 <a,c> 后会使 a,b,c 构成一个环，此时 <a,c> 的存在毫无价值，反而会增大总权值。其次是终止条件的判断，我们需要选择多少条边呢？答案是 n-1 条，很容易证明，在不存在环 的情况下，只需要 n-1 条边就能构成 n 个顶点的连通图。

有了以上基础，就能实现我们的算法了：先将所有边根据权值升序排序。然后从最小边开始选择，若不会与已有边形成环，则加入生成树。重复以上过程，直到边数达到 n-1 条。

现在的问题就只剩如何判断环了。要如何判断环呢？其实很简单，只需要对当前边 的起点与终点，判断其在已选择路径 中是否存在公共起点就行了。还是刚才的例子，对于边 <a,c> ，起点a在已选择路径 <a,b> <b,c> 中的起点为a，而终点c顺着b可以找到起点a，这时就说明a和c在已选择路径中拥有公共起点。那么再加入 <a,c> 就会构成环。

针对上述算法，聪明的你一定能猜到，这需要用到并查集 来实现。

代码实现

由于Kruskal是对边进行操作，所以在读取邻接关系的时候要针对边进行存储：

typedef struct Edge
{
    int start;  //起点
    int end;    //终点
    int weight; //权值
} Edge;
vector<Edge *> edges;         //边数组,用于kruskal算法

然后准备一个排序函数，用于作为STL中sort的参数，对边进行依权值升序排序：

bool sortByWeight(Edge *edge1, Edge *edge2)
{
    return edge1->weight < edge2->weight;
}

当然还需要先写一个并查集，~~但我这边偷懒就不写了~~，可以翻阅之前的笔记查看。有了以上准备，就可以开始我们的算法了。首先定义几个参数：

1
2
3

int cost = 0; //总权值
int k = 0;    //已经选中的边的个数,当选中[顶点个数-1]条边就结束
UFSet ufset(vertex_num);  //并查集

首先对边进行排序：

1	sort(edges.begin(), edges.end(), sortByWeight);

接下来按权值从小到大的顺序，对每条边进行判断：如果起点与终点具有共同起点，即并查集find()得到的祖先为相同点，那就忽略不计；否则将其加入mst，并将该边的起点与终点merge()，即将选中边加入已选择路径。不断循环以上过程，直到选择的路径为 n-1 条，结束搜索：

for (auto i : edges) //对每条边,如果不会与已选择边构成环路就是可用通路
{
    if (ufset.find(i->start) != ufset.find(i->end))
    {
        cout << vertexs[i->start] << "->" << vertexs[i->end] << ':' << i->weight << endl;
        cost += i->weight;
        ufset.merge(i->start, i->end);
        k++;
    }
    if (k == vertex_num - 1)
        return cost;
}

完整代码

//whuangOJ-1607
//LOJ-#123
//luogu P3366
#include <iostream>
#include <algorithm>
using namespace std;

struct edge
{
    long long start, end, weight;
} edges[500005];
int fa[200005];
void init(int n)
{
    for (int i = 1; i <= n; i++)
        fa[i] = i;
}
int find(int x)
{
    return x == fa[x] ? x : (fa[x] = find(fa[x]));
}
void merge(int x, int y)
{
    fa[find(x)] = find(y);
}
bool cmp(edge x, edge y)
{
    return x.weight < y.weight;
}
int main()
{
    int n, m;
    cin >> n >> m;
    init(n);
    for (int i = 0; i < m; i++)
        cin >> edges[i].start >> edges[i].end >> edges[i].weight;
    sort(edges, edges + m, cmp);
    long long cost = 0;
    int k = 0;
    for (int i = 0; i < m; i++)
    {
        if (find(edges[i].start) != find(edges[i].end))
        {
            cost += edges[i].weight;
            merge(edges[i].start, edges[i].end);
            k++;
        }
        if (k == n - 1)
            break;
    }
    cout << cost << endl;
    return 0;
}