前面几个算法基本是以无向图为基础的，这次我们就来聊一聊有向图。

我们这次来解决两种问题：事件序列的执行顺序以及判断有向图中是否存在环。

以上两种问题都可以通过 拓扑排序(Topological Sort) 来解决。

引入

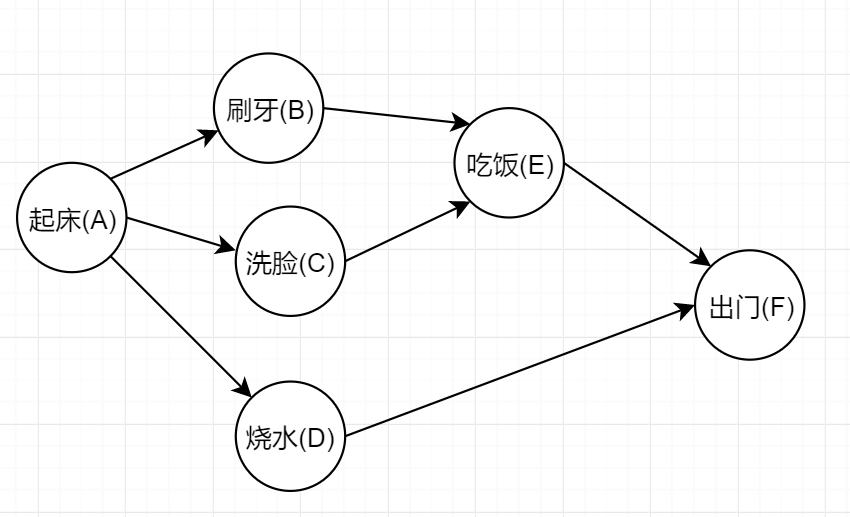
假设上图是你起床到出门的过程需要完成的事件序列，那么要如何给出一个符合约束的执行顺序呢？

作为人类，肯定很容易就能看出来 A->B->C->D->E->F 或者 A->C->B->E->D->F 都是可行的执行顺序，但计算机没办法一眼看出来。我们便可以用拓扑排序计算出这样的一个拓扑序列。

拓扑排序

算法简介

其实上方的这种图我们一般称为 AOV网 （Activity On Vertex network），即将每个顶点都记为一个活动，与之对应的为 AOE网（Activity On Edge network），这两种网都是建立在 DAG图 （有向无环图Directed Acyclic Graph）之上的。

对于这种图，我们可以计算出一条符合事件发生次序的序列，名为 拓扑序列 ，这其中的过程则称为 拓扑排序 。

其基本思想是利用每个点的 入度 ：入度为 0 的点是没有任何前置事件的，即可直接执行。而执行完当前事件后，就将 其与其所连边 抛开不管，将问题转换成去除这个点后的网的拓扑排序问题。换句话说，就是将它所指向的点的入度减一，再判断是否有入度为 0 的点，重复这个过程直到没有点可取为止。

对上方那个例子，一开始的时候只有 A 点的入度为 0 ，所以将其记录下来并去除（标红的即为最终序列）：

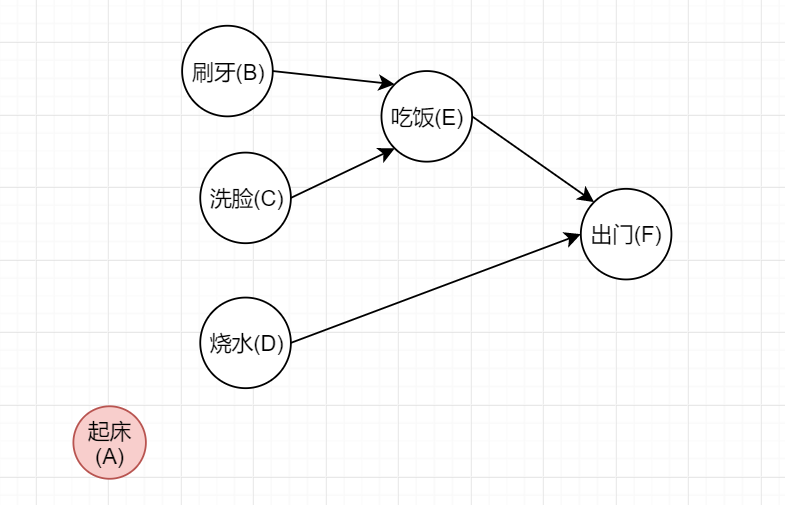
此时有 BCD 三点的入度都为 0 ，所以可以分别取出：

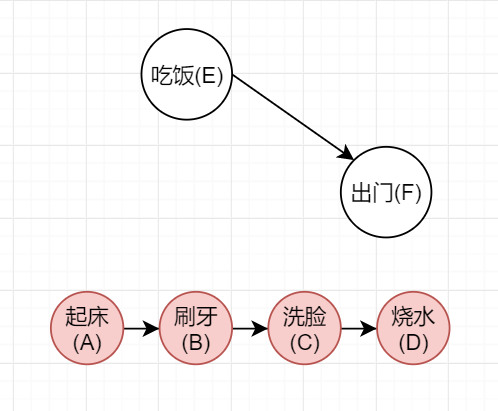
最后就是取出 E ，然后是最后的 F。此时再没有点可以取了，也就说明得出了最后的序列：A->B->C->D->E->F。

代码实现

这个算法很容易让我们联想到 BFS 的思想，所以为了防止多次重复遍历，我们可以用一个队列来实现。

首先我们要创建一个 inDegree[vertex_num] 数组来记录每个顶点的入度，在创建邻接表的过程中就应该读入数据，这里不多赘述。

第一轮先将现有的入度为 0 的点入队：

1
2
3
4
queue<int> temp;
for (int i = 0; i < vertex_num; i++) //入度为0的记录下来
    if (inDegree[i] == 0)
        temp.push(i);

然后进行循环：

1
2
3
4
5
6
7
8
9
10
11
12
while (!temp.empty())
{
    int curVex = temp.front();
    temp.pop();
    for (int i : adjacent[curVex]) //找到当前结点指向的所有结点,将其入度-1,若入度为0便入队
    {
        inDegree[i]--;
        if (inDegree[i] == 0)
            temp.push(i);
    }
    cout << vertexs[curVex] << "->";
}

至此，算法结束。是不是很简单，简单到我都不想做过多的解释了……

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void AdjacencyList::topologicalSort()
{
    queue<int> temp;
    for (int i = 0; i < vertex_num; i++) //入度为0的记录下来
        if (inDegree[i] == 0)
            temp.push(i);
    while (!temp.empty())
    {
        int curVex = temp.front();
        temp.pop();
        for (int i : adjacent[curVex]) //找到当前结点指向的所有结点,将其入度-1,若入度为0便入队
        {
            inDegree[i]--;
            if (inDegree[i] == 0)
                temp.push(i);
        }
        cout << vertexs[curVex] << "->";
    }
    cout << "EXIT" << endl;
}

应用——有向无环图

拓扑排序一个十分重要的应用就是判断有向图中是否存在 环 。容易发现：如果图中存在环，那在拓扑排序的过程中环内任何一点的入度都不可能为 0。换言之，得出的拓扑序列无法涵盖所有顶点。这样就能轻松判断图中是否有环：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void AdjacencyList::topologicalSort()
{
    queue<int> temp;
    int curVerNum = 0;                   //当前已选择的顶点数
    for (int i = 0; i < vertex_num; i++) //入度为0的记录下来
        if (inDegree[i] == 0)
        {
            temp.push(i);
            curVerNum++;
        }
    while (!temp.empty())
    {
        int curVex = temp.front();
        temp.pop();
        for (int i : adjacent[curVex]) //找到当前结点指向的所有结点,将其入度-1,若入度为0便入队
        {
            inDegree[i]--;
            if (inDegree[i] == 0)
            {
                temp.push(i);
                curVerNum++;
            }
        }
    }
    if (curVerNum != vertex_num)
        cout << "There is a loop.\n";
}