二叉排序树(Binary Sort Tree),又称二叉查找树(Binary Search Tree),亦称二叉搜索树。是数据结构中的一类。在一般情况下,查询效率比链表结构要高。
二叉排序树,顾名思义,是一种能将数据进行排序的二叉树。其 中序遍历 所得出的序列为有序序列。以下我们统一以 升序序列 进行讨论,降序序列原理相同。
要实现一棵这样的树,只要遵循一条规则: 每个结点的左子结点的值小于当前结点,右子结点的值大于当前节点 。具体为什么要这样?假设一个结点 A (A->left=B; A->right=C) ,中序遍历得到的序列为 BAC ,要符合升序排列,必定是 B<A<C。
二叉树的基本结构之前聊过多次,这里就不多赘述了
1
2
3
4
5
6
7
8
| class BinaryTree {
typedef struct Node {
int val;
Node* left;
Node* right;
} Node, *BTLink;
BTLink root;
}
|
插入数据
要构造一棵排序二叉树,自然要从插入数据开始,在插入数据的时候,只需要遵从上面那句基本规则即可:
1
2
3
4
5
6
7
8
9
10
| void BinaryTree::insert(int val, BTLink& node) {
if (!node) {
node = (BTLink)malloc(sizeof(Node));
node->val = val;
node->left = node->right = NULL;
return;
}
if (node->val == val) return;
val < node->val ? insert(val, node->left) : insert(val, node->right);
}
|
这里我们通过递归的方法找到当前值应该存放的位置,然后将其置于那个位置即可。
查找数据
查找数据的过程其实已经隐含在插入数据的过程中了,只需对树进行递归查找:
1
2
3
4
5
| bool BinaryTree::find(int val, BTLink node) {
if (!node) return 0;
if (node->val == val) return 1;
return val < node->val ? find(val, node->left) : find(val, node->right);
}
|
删除数据
较之前面两部分操作,删除数据的操作比较麻烦。由于删除数据后要保持二叉排序树结构的 稳定 (就是保证删除后还能拥有原本的性质),我们需要在删除后进行一些平衡的操作。由于被删除的数据结点有三种情况:
- 叶结点
- 只有一个子结点的结点
- 有两个子结点的结点
所以我们要对这三种情况分别讨论。
但在这之前,我们要先做一些前期的准备。首先要通过该数据找到其对应结点:
1
2
3
4
5
6
7
8
9
10
11
12
| void BinaryTree::remove(int val) {
findCurNode(val, root);
}
void BinaryTree::findCurNode(int val, BTLink& node) {
if (!node) return;
if (node->val == val) return removeNode(node);
val < node->val ? findCurNode(val, node->left) : findCurNode(val, node->right);
}
void BinaryTree::removeNode(BTLink& node) {
if (!node) return;
}
|
然后就可以进行分类删除了:
叶结点
要删除叶结点最为简单,毕竟不会影响到其它结点的顺序。只需要做简单的 free() 操作:
1
2
3
4
5
| if (!node->left && !node->right) {
free(node);
node = NULL;
return;
}
|
只有一个子结点的结点
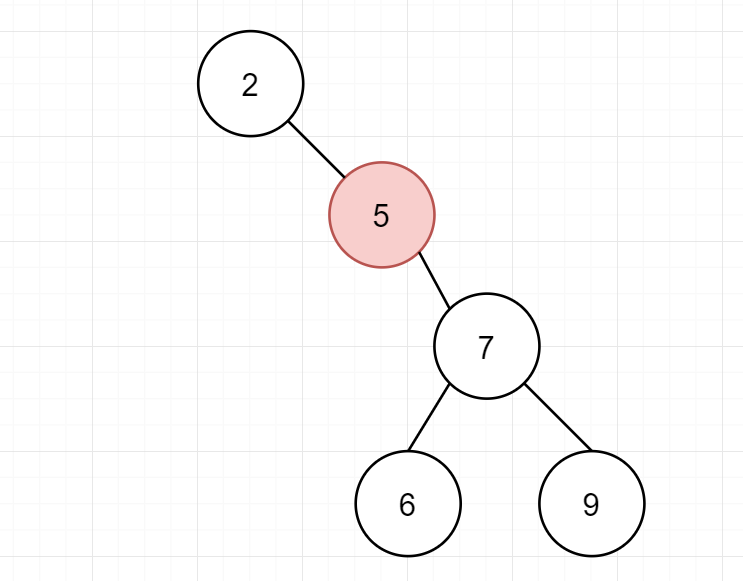
对于这种结点,我们只需将其所在位置换成其子结点即可:
1
2
3
4
| BTLink temp = node;
node = node->left ? node->left : node->right;
free(temp);
return;
|
有两个子结点的结点
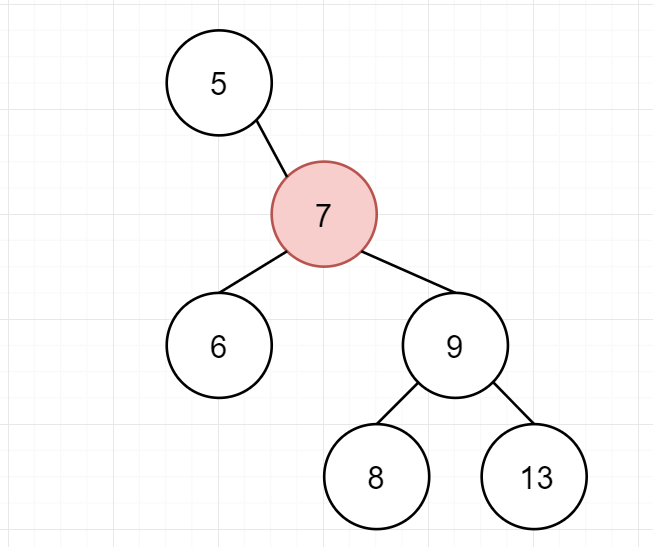
1
2
3
4
5
6
7
8
9
10
11
12
| BTLink temp = node->right, previous = temp;
while (temp->left) {
previous = temp;
temp = temp->left;
}
node->val = temp->val;
if (temp == previous)
node->right = temp->right;
else
previous->left = temp->right;
free(temp);
return;
|
我们接下来对上述代码慢慢分析:
要删除这样的结点,最简单的方式就是找到一个能替代它的数据。要能放在这个位置,首先需符合二叉排序树的性质,很容易想到,应该使用升序序列中的前一个或后一个值来代替它,这里我们选择后一个值,即中序遍历的后继结点,当然,选择前驱结点也是可以的。
首先找到其后继结点以及其后继结点的父结点:
1
2
3
4
5
| BTLink temp = node->right, previous = temp;
while (temp->left) {
previous = temp;
temp = temp->left;
}
|
然后将后继结点的值覆盖到当前结点上 node->val = temp->val; ,好的,当前的数据就这样被我们删除了,接下来将后继结点删除掉即可(不然后继的数据会出现两次)。注意观察后继结点的性质,会发现它一定不存在左子树,也就是说,它只有一个子结点。那就好办了,只需要将其右子树放在正确的位置即可:
1
2
3
4
| if (temp == previous)
node->right = temp->right;
else
previous->left = temp->right;
|
最后 free(temp); ,完成删除操作。
完整代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
|
#include <bits/stdc++.h>
using namespace std;
class BinaryTree {
typedef struct Node {
int val;
Node* left;
Node* right;
} Node, *BTLink;
BTLink root;
void insert(int val, BTLink& node);
bool find(int val, BTLink node);
void findCurNode(int val, BTLink& node);
void removeNode(BTLink& node);
void midOrder(BTLink node);
public:
BinaryTree();
void insert(int val);
bool find(int val);
void remove(int val);
void midOrder();
};
int main() {
int nums[] = {1, 4, 5, 5, 6, 6, 6, 6, 6, 6, 6, 6, 6, 8, 9, 10, 0, 1, 2, 4, 3};
BinaryTree t;
for (auto i : nums) t.insert(i);
for (auto i : nums) {
t.remove(i);
t.midOrder();
}
}
BinaryTree::BinaryTree() {
root = NULL;
}
void BinaryTree::insert(int val) {
insert(val, root);
}
void BinaryTree::insert(int val, BTLink& node) {
if (!node) {
node = (BTLink)malloc(sizeof(Node));
node->val = val;
node->left = node->right = NULL;
return;
}
if (node->val == val) return;
val < node->val ? insert(val, node->left) : insert(val, node->right);
}
bool BinaryTree::find(int val) {
return find(val, root);
}
bool BinaryTree::find(int val, BTLink node) {
if (!node) return 0;
if (node->val == val) return 1;
return val < node->val ? find(val, node->left) : find(val, node->right);
}
void BinaryTree::remove(int val) {
findCurNode(val, root);
}
void BinaryTree::findCurNode(int val, BTLink& node) {
if (!node) return;
if (node->val == val) return removeNode(node);
val < node->val ? findCurNode(val, node->left) : findCurNode(val, node->right);
}
void BinaryTree::removeNode(BTLink& node) {
if (!node) return;
if (!node->left && !node->right) {
free(node);
node = NULL;
return;
}
if (node->left && node->right) {
BTLink temp = node->right, previous = temp;
while (temp->left) {
previous = temp;
temp = temp->left;
}
node->val = temp->val;
if (temp == previous)
node->right = temp->right;
else
previous->left = temp->right;
free(temp);
return;
}
BTLink temp = node;
node = node->left ? node->left : node->right;
free(temp);
return;
}
void BinaryTree::midOrder() {
midOrder(root);
cout << endl;
}
void BinaryTree::midOrder(BTLink node) {
if (node) {
if (node->left) midOrder(node->left);
cout << node->val << ' ';
if (node->right) midOrder(node->right);
}
}
|









