归并排序与快速排序都运用了分治(divide-and-conquer)的思想,将一整段序列的排序划分为多段子序列的排序问题。这两个算法的划分法都是二分,最后可以达到 O(nlogn) 的效率(本文中的效率与复杂度取的都是平均值)。
归并排序
归并
首先要了解一下归并算法:给出两个升序序列,将其合并成一个新的升序序列,要怎么做?
如果将其简单组合再进行排序,未免太低效。我们可以利用其本身就升序的特性,每次先从两个序列头部取出较小的值,置于新序列的头部,并重复该步骤,直到两原序列都为空,算法结束,时间复杂度为 O(n) 。
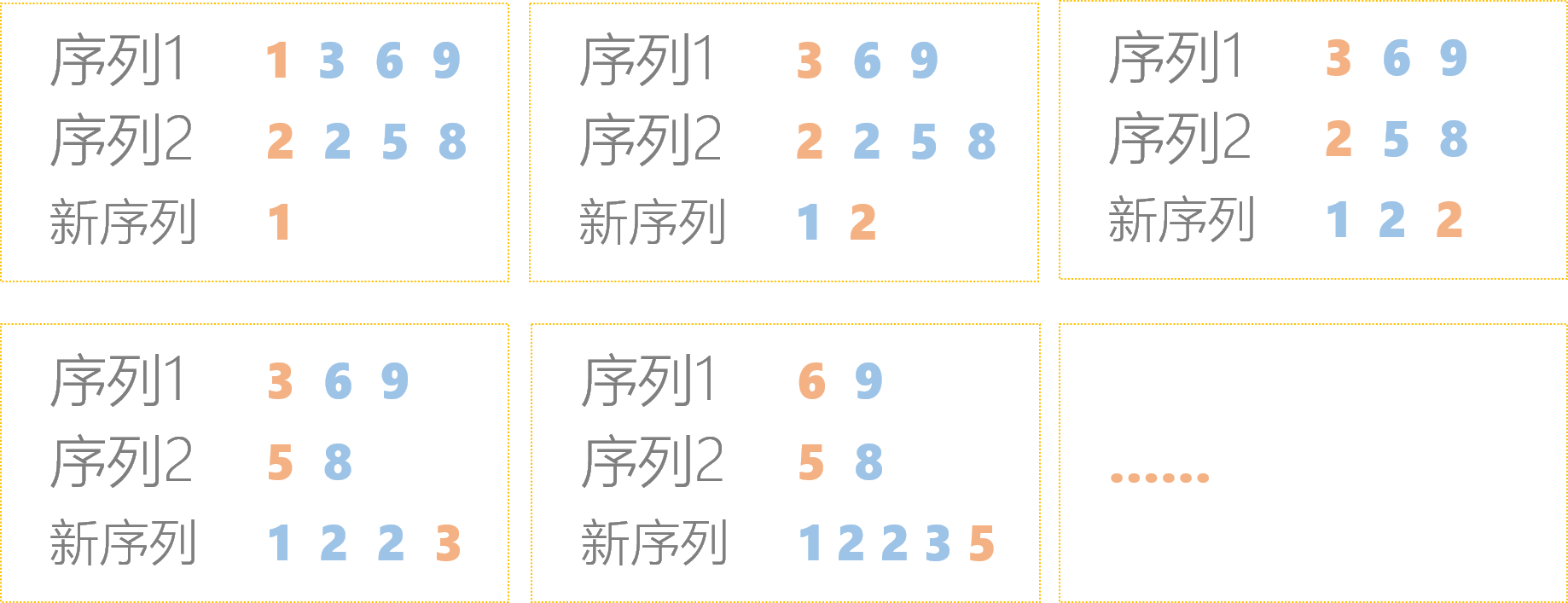
归并排序
归并排序就是用了归并的思想:将一个序列分成两段,这两段 分别有序 ,那就可以对其进行归并,得到完整的有序数组。那么要怎么保证这两段序列分别有序呢?很简单,对其分别递归执行归并排序就可以了。由于这样分块执行的次数为 logn (即log(2)(n))次,所以完整的归并排序时间复杂度为 O(nlogn) 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
template <class Type>
void MergeSort(Type arr[], int n) {
Type* temp = (Type*)malloc(n * sizeof(Type));
MergeSort_rec(0, n - 1, arr, temp);
}
template <class Type>
void MergeSort_rec(int st, int ed, Type arr[], Type temp[]) {
if (st < ed) {
int mid = st + (ed - st) / 2;
MergeSort_rec(st, mid, arr, temp);
MergeSort_rec(mid + 1, ed, arr, temp);
int i = st, j = mid + 1, k = st;
while (i <= mid && j <= ed) temp[k++] = arr[i] < arr[j] ? arr[i++] : arr[j++];
while (i <= mid) temp[k++] = arr[i++];
while (j <= ed) temp[k++] = arr[j++];
for (i = st; i <= ed; i++) arr[i] = temp[i];
}
}
|

快速排序
快速排序的基本思路是:先取出一个 基准值 pivot,然后把所有小于它的值放在它左边,大于它的值放在它右边,接着分别对左边和右边的序列重复递归执行该过程,最终使得序列有序。
我主要介绍一下单次执行中如何把小于基准值的值置左,大于的置右:首先我们取序列第一位为基准值,然后有两个箭头,分别指向序列的最左边与最右边(除去基准值的部分)。首先是右指针向左移动,直到找到一个小于基准值的数,将其置于基准值原本的位置,接着是左指针向右移动,找到一个大于基准值的数,将其置于上一个数原本的位置(即右指针当前指向位置)。然后右指针左移,找数,填坑;左指针右移,找数,填坑……直到左右指针相遇,便将基准值填入最后这个坑。一轮算法结束:

由于平均情况下需要 logn 次递归执行,而每次执行又只需遍历一遍序列,所以其时间复杂度也为 O(nlogn) 。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
template <class Type>
void QuickSort(Type arr[], int n) {
QuickSort_rec(0, n - 1, arr);
}
template <class Type>
void QuickSort_rec(int st, int ed, Type arr[]) {
if (st < ed) {
int i = st, j = ed;
Type temp = arr[i];
while (i < j) {
while (i < j && arr[j] >= temp) j--;
arr[i] = arr[j];
while (i < j && arr[i] <= temp) i++;
arr[j] = arr[i];
}
arr[i] = temp;
QuickSort_rec(st, i - 1, arr);
QuickSort_rec(i + 1, ed, arr);
}
}
|










