图形学学习笔记#2:明暗着色
概述
理论上来说,正确的明暗处理需要全局的计算,但这样与流水线模型的处理方式相悖,所以我们处理光照的时候应该用局部光照来对全局光照进行逼近。
光线从光源表面离开有两种方式: 自发射 和 反射 。这两种方式从光源表面一点 (x, y, z) 离开时均可用发射方向 与波长 来进行表示:照明函数 。
一个光源能发射出不同量的不同频率的光,其方向都有可能不同,所以对其进行计算的时候要用RGB三种成分进行分别计算,由此可以得知光亮度函数 。
光源
光源的亮度函数都要分成RGB三种成分分别计算,下文不再赘述,直接给出通用的计算方法。
点光源
若从点 发出点光源,照射到一点 ,则在该点接收到的光强与距离的平方成反比。
点光源在图形学中被大量使用,因为使用起来很方便。但其无法很好地反映现实,因为得到的图像对比度较高,而真实光源应较柔和。
真实光照
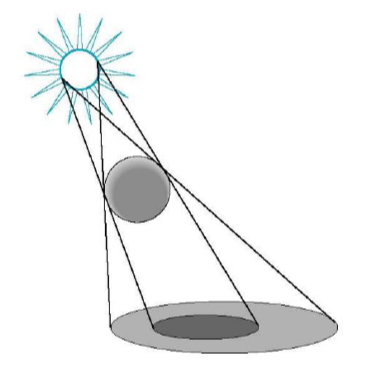
真实光照的光源较大,所以阴影分为 本影 与 半影 两部分,这是点光源无法实现的。但可以在点光源中加入环境光来降低高对比度的问题。
聚光灯
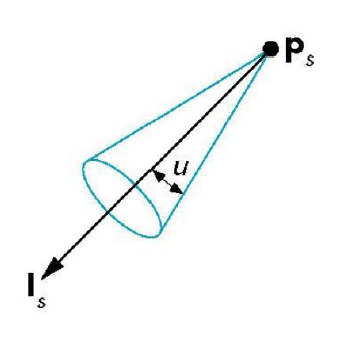
当 u=180° 时,聚光灯成为点光源。
聚光灯的照明强度函数是光源到表面上某点向量s与中心轴夹角 的函数,一般定义为 。
无穷远光源
可视为平行光源,比如太阳。
环境光
亮度由 确定,在每一点的值完全相同,但各个表面对环境光的反射会有不同,有:镜面(入射光被部分吸收,其余全部单一角度反射)、漫反射面(把光线均匀散射到各方向)和透明面(部分进入表面,发生折射,部分被反射),每个场景中对象的表面可以是这三种情形的任一种或多种综合。
Phong光照模型
Phong模型可以用来快速地计算局部光照,分为 漫反射光 、 镜面反射光 与 环境光 三类分量。其中,要使用四个向量: 入射光方向l 、 视点方向v 、 法向量n 以及 理想反射方向r 。当然,RGB三原色都要分别计算这三种分量。
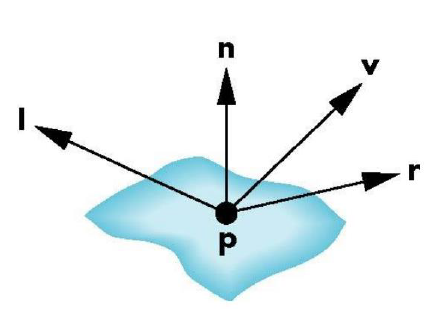
理想反射
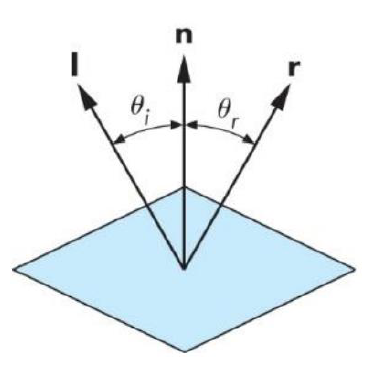
当l、n与r均为单位向量时:
计算原理不难,不多赘述,就强调一个细节: 。
鉴于问的人比较多,我还是稍微多介绍几句这个计算过程吧。
对于 这一项,其实只有n是作为方向存在, 只是算出单位向量l在n上的投影的长度,然后乘上只用于计算方向的单位向量n,来确定这一条向量。
漫反射
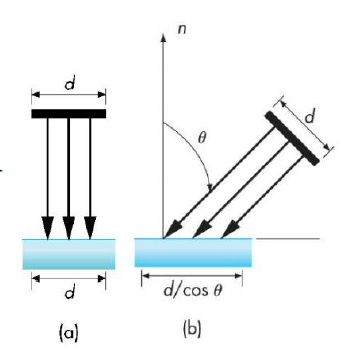
很显然,光照的面积与光强成反比关系,所以照到对象上的光强为 ,但对于漫反射来说,并非所有的光都会反射,所以记反射比例系数为 ,可知: ,但由于这个cos值只能为正数,所以一般将该公式写作:
镜面光
大多数的曲面其实并不能理想漫反射,也不能理想反射,而是镜面,要用镜面光模型来计算。
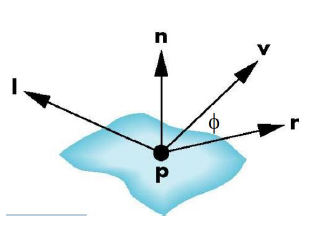
记 为高光系数,则 (别问为什么是这样,我也不懂,记住就行了),即:
这里聊一聊高光系数,取值在510的话,材料类似于塑料;100200对应于金属;趋向无穷大时极为镜面。
环境光
环境光的量与颜色依赖于光源的颜色和对象的材料属性:
距离项
在前文有提到过,光源到达对象表面的光强与距离成反比,所以对于 漫反射项 与 镜面项 ,我们需要添加一个二次的距离衰减因子: 。
总结
考虑到以上提到的三类分量与每类分量的三种原色,每个点光源有9个光强系数,以及对应材料属性的9个反射系数,和一个高光系数。根据这些系数与距离衰减因子,可以表示出Phong光照模型:
改进
在上文介绍的镜面光项计算中有个小问题,对于每个点来说,需要独立地计算视点向量v与反射向量r,而Blinn给出了一个效率更高的计算方法:通过中值向量来代换。
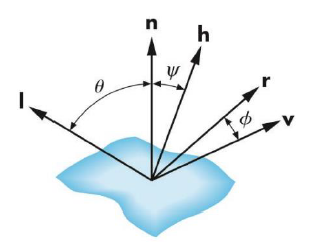
记 ,即l与v的中值单位向量,易证: (证明给在下方),所以可以用 代替 。
的证明
多边形明暗处理
多边形明暗处理,顾名思义,就是对多边形整体进行明暗处理。由于我们交给代码的一般只会是几个顶点,而多边形内部的信息无法直接获得,要进行明暗处理便相对复杂,这部分就是来解决这个问题的。
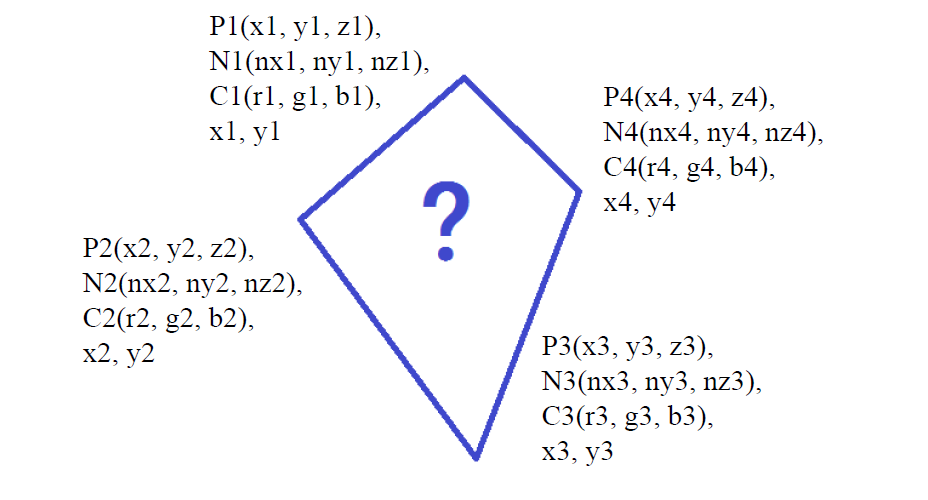
对于一个多边形来说,每个点有P(位置)、N(法向量)与C(颜色)三个信息,而对于多边形内部的点,其位置可以通过顶点的坐标变换求得,法向量可以通过相邻平面求法向平均求得,那么问题在于颜色,每个内部点的颜色要如何求,一般有三种方法:
平面着色法
平面着色法也就是OpenGL的api中的 glShadeModel(GL_FLAT) ,是假设视点在无穷远的位置,从而将视点方向与入射方向都视为常向量,同时由于同一多边形上的法向本身为常向量,所以对于每个多边形,均可用一点的颜色来代替其他所有点的颜色。这样模拟出来的效果较差,特别是当多个点色差大时,会显得及其突兀。
Gouraud着色
线性插值
在介绍Gourand着色前,我们先简单介绍一下线性插值。
假设在一维平面上相距为 的两点坐标分别为 , ,则与 相距长度 的点的坐标可以被线性表示为 ,在其他非均匀量的计算上如果也这样用均匀量来模拟,则称为线性插值。
同理,在二维平面的三角形 中,任意一点均可表示为 ,其中 ,这便是平面上的线性插值。
Gouraud着色算法
Gouraud的算法正是对颜色信息进行了双线性插值,将每一个多边形自上而下扫描。对于每一条扫描线来说,与多边形会有左右两个交点 ,通过线性插值计算出这两个颜色后,再通过这两个点的颜色进行线性插值来计算该扫描线上每一点的颜色。
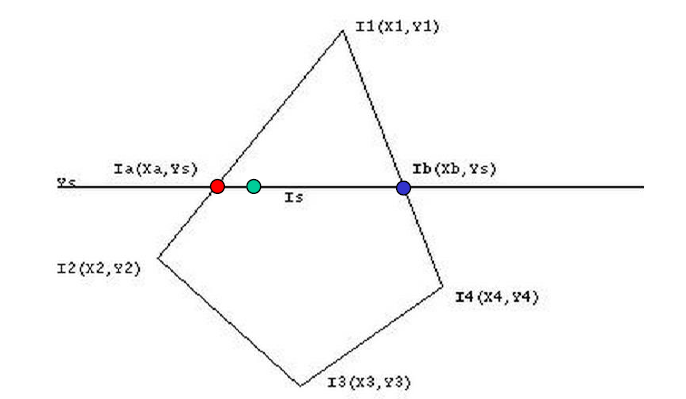
这样的做法比起平面着色法来说更为精致,至少在每个平面上会有均匀的渐变效果。然而,该做法也会出现问题,问题在于线性插值法本身的数学误差。线性插值用解析几何的角度来解释便是将两点坐标用线段相连,但若这两点间本身并非均匀(如高光),则便会将该峰值抹平,造成 高光丢失 。
Phong着色
最后介绍一下能解决以上问题的着色方法:Phong着色。不同于Gouraud的对颜色进行插值,Phong着色采用对 法向 进行插值,再对插值的法向计算光照的方法。
很显然,使用这种方法计算出的图形会更加光滑,但是计算法向的过程较复杂,所以该算法的复杂度较高。







