要考试了，好累喔。把一些细节的东西稍微整理一下，不属于任何专题，但是应该也蛮有用的。

光

光，落在你脸上。可，爱一如往常。

可见光的波长：350~780nm。

  • 红色：650nm
  • 蓝色：450nm
  • 绿色：520nm

颜色系统

加色系统

RGB red green blue

基于自身发光的颜色系统（肯定是自身发光才能加嘛）

显示器、投影仪、照片正片……

减色系统

CMY cyan magenta yellow

基于反光的颜色系统（颜色被吸收掉了一部分，所以是减）

彩色打印、照片负片……

针孔摄像机

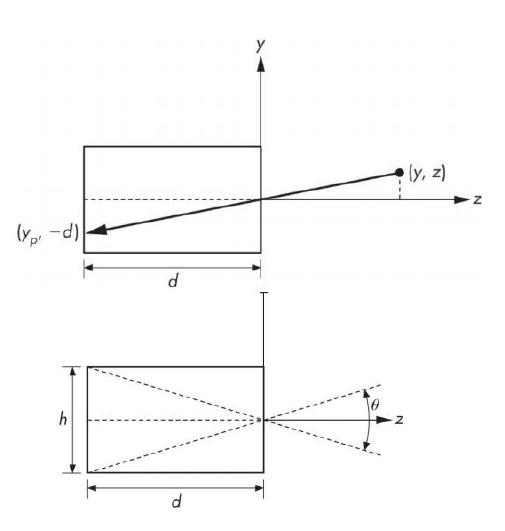
(x,y,z)(x,y,z)点的投影(xp,yp,−d)(x_p,y_p,-d)

xp=−d∗xz,yp=−d∗yzx_p=\frac{-d*x}{z},y_p=\frac{-d*y}{z} （这两个怎么推导的应该不用说了，不会的话就去重修小学数学吧……）

视域：胶片上能成完整像的最大物体所张的角度 θ=2tan⁡−1(h2d)\theta=2\tan^{-1}(\frac{h}{2d})

图像

图像生成四要素：几何、材质、光照、观察者。

图形渲染流水线

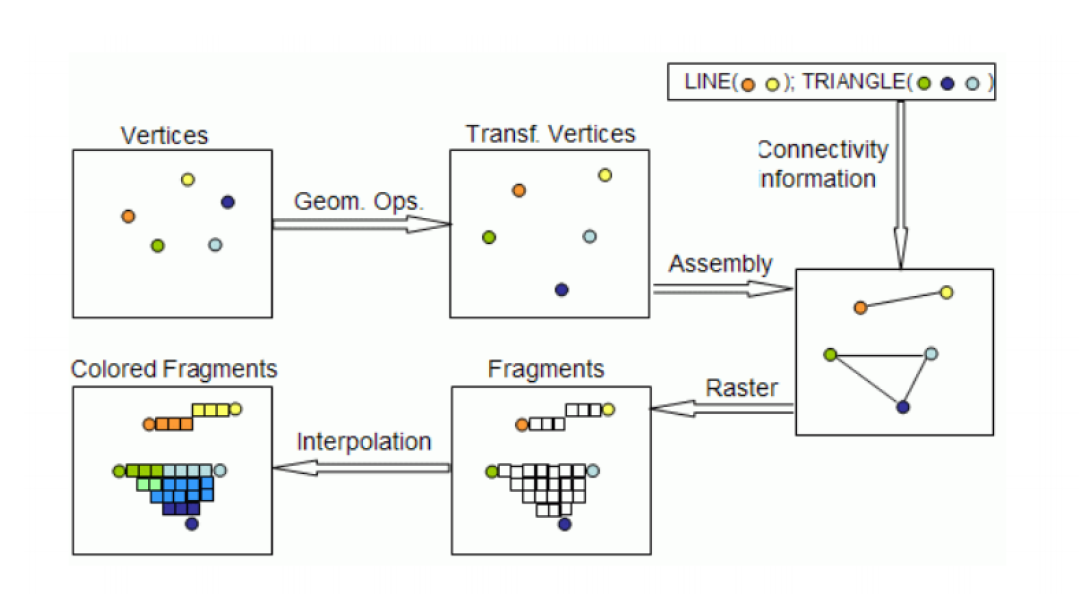
渲染流水线分为四个主要步骤：顶点处理、裁剪和图元装配、光栅化、片段处理。

  1. 顶点处理，就是进行坐标系变换，也就是之前提过的视图变换视口变换和投影之类的。
  2. 图元装配，就是把顶点组装成几何对象。而裁剪，就是将不在视景体中的对象裁剪掉。
  3. 光栅化，对于还没被裁剪的对象们，将在这一步在帧缓冲区中被赋予颜色。光栅化程序在对象上对顶点的属性进行插值得到片段的属性。
  4. 片段处理，对片段进行处理，以确定帧缓冲区中相应像素的颜色。隐藏面消除也是在这一步执行的。

隐藏面消除

隐藏面消除一般有两种途径：

  • 多边形拣选：即将图元不可见的表面剔除，比如反面。
  • 深度缓存算法(Zbuffer)：增加额外的深度缓存空间来保存图元的深度信息，然后判断其遮挡效果。

图像卷积

数字图像是一个二维的离散信号，对数字图像做卷积操作其实就是利用卷积核（卷积模板）在图像上滑动，将图像点上的像素灰度值与对应的卷积核上的数值相乘，然后将所有相乘后的值相加作为卷积核中间像素对应的图像上像素的灰度值，并最终滑动完所有图像的过程。

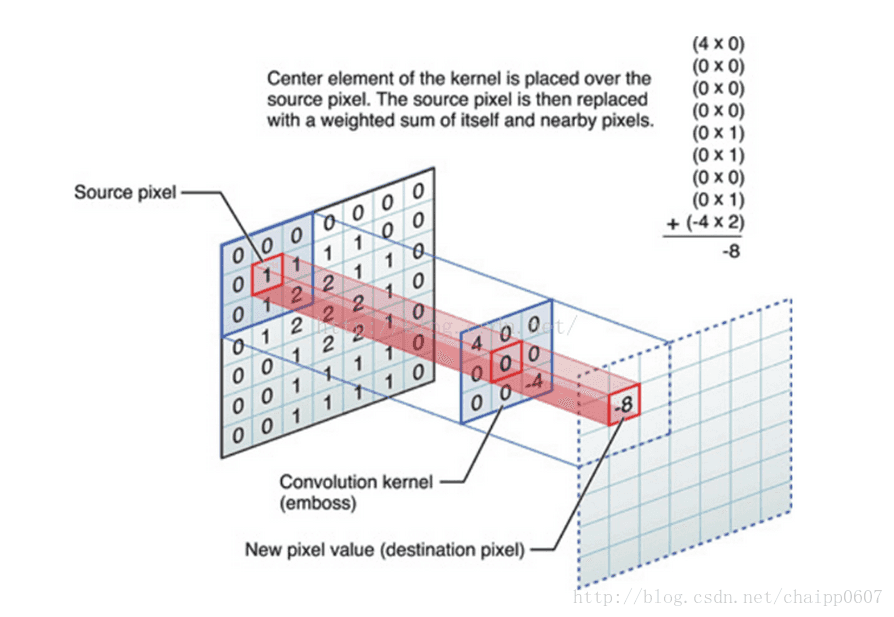
卷积核一般要求是奇数阶，才方便对中心点进行处理。同时，卷积核所有元素之和的大小决定了卷积后图像的亮度，若和正好为1，则可保证亮度守恒。

边界补充

回到上面那张图，原本7阶的图像，经过一轮卷积后，大小就变成了5阶，存在边缘损失，所以我们需要在卷积前先对其进行边界补充，扩展为9阶，从而保证卷积后图像大小的守恒。

一般有以下几种补充方法：

  • 补零：即将补充出的部分全部置零
  • 复制：即从最接近原图的部分开始补充，补充的值为与原图临近点的值
  • 镜像：与复制相似，不过取的是镜像
  • 块：就是整块地复制原图像

卷积核

下面稍微介绍几种常用的卷积核

均值滤波

1/91/91/91/91/91/91/91/91/9\begin{array}{ccc} 1/9 & 1/9 & 1/9 \\ 1/9 & 1/9 & 1/9 \\ 1/9 & 1/9 & 1/9 \\ \end{array}

取平均值来代替中间值，用来平滑图像。

锐化

−1−1−1−19−1−1−1−1\begin{array}{ccc} -1 & -1 & -1 \\ -1 & 9 & -1 \\ -1 & -1 & -1 \\ \end{array}

或

0−10−15−10−10\begin{array}{ccc} 0 & -1 & 0 \\ -1 & 5 & -1 \\ 0 & -1 & 0 \\ \end{array}

Prewitt边缘检测

−101−101−101\begin{array}{ccc} -1 & 0 & 1 \\ -1 & 0 & 1 \\ -1 & 0 & 1 \\ \end{array}

水平梯度卷积，用于检测水平边缘。同理还有垂直梯度卷积，就是把它旋转90°，永远检测垂直边缘。

Soble边缘检测

−101−202−101\begin{array}{ccc} -1 & 0 & 1 \\ -2 & 0 & 2 \\ -1 & 0 & 1 \\ \end{array}

Soble卷积核与Prewitt卷积核类似，都是用来检测水平边缘，但Soble更强调与边缘相邻的像素点对边缘的影响。

Laplacian边缘检测

−1−1−1−18−1−1−1−1\begin{array}{ccc} -1 & -1 & -1 \\ -1 & 8 & -1 \\ -1 & -1 & -1 \\ \end{array}

在锐化的同时也做了边缘检测，同时不局限于水平或垂直方向。

几何

贝塞尔曲线

本质上是对n个点执行n-1次线性插值所得到的点连成的曲线。（细节不谈，实验刚手写过，不可能有人记不住吧）

生成系数即为n-1阶二项展开系数

PBezier(t)=∑Pin!i!(n−i)!(1−t)n−itiP_{Bezier}(t)=\sum P_i \frac{n!}{i!(n-i)!}(1-t)^{n-i}t^i

距离场(SDF)

距离场的概念应该不用多介绍了，与之相似的还有截断符号距离场TSDF。

点云→SDF：

  • 对于每个体素，计算其与点云的最近距离
  • 根据点云的法向判断内外（不过好像对正负没有明确要求，只要统一应该就可以了）

SDF→点云：

  • 找到临界点并插值（也就是在图里的正负分界线稍微画一下就行）

SDF的优点：便于卷积，整体性强，不容易受噪声干扰，适合用于数据的融合。

SDF的缺点：数据量大， 往往需要稀疏表示

网格

M=<V,E,F>M=<V,E,F>

这里有两个不重要结论： F≈2V,F+V=E+2F\approx 2V, F+V=E+2

拓扑

二维流形：简单点说就是，一个表面，当用一个小球去切割时，得到一个二维的圆盘。

网格去噪

拉普拉斯算子： 1∣Ni∣(∑pj)−pi\frac{1}{\left| N_i \right|}(\sum p_j)-p_i ，简单点说就是，一个点与他周围点的平均值的差值。

动画

BlendShape

BlendShape实际上就是定义一组关键形状，比如人脸的各个表情，然后通过其线性组合得到新的形状，新的表情。

动作捕捉

动作捕捉里有两个比较重要的概念：前向运动学Forward Kinematics与反向运动学Inverse Kinematics。

  • 前向运动学是已知人体的姿态，并根据父骨骼到子骨骼的顺序逐级向下求出一个个端点的位置。
  • 反向运动学则是已知端点位置，通过这些位置的关系求出整体的姿态与对象。

弹簧模拟

f=−[ks(∣p1−p2∣−l0)+kd((v1−v2)⋅(p1−p2)∣p1−p2∣)]⋅(p1−p2)∣p1−p2∣f=-[k_s(\left|p_1-p_2\right|-l_0)+k_d(\frac{(v_1-v_2)\cdot(p_1-p_2)}{\left|p_1-p_2\right|})]\cdot\frac{(p_1-p_2)}{\left|p_1-p_2\right|}

ksk_s 那一项我能理解，最后的方向项我也能理解，但是 kdk_d 那一项真的没看懂……有没有物理学得好的朋友来给我解释一下？

通过这一个弹簧受力公式，加上各基本运动规律，就能求出每个时刻的弹簧端点位置，从而模拟出一根弹簧。把更多的弹簧穿起来，就能够模拟出布料系统。具体的计算就不多介绍，理解原理就很容易能算出来了。