Histogram Equalization

一张图片的直方图如果不均衡，会显得偏亮、偏暗、甚至是整体偏灰。Histogram Equalization的算法可以将一张图片的直方图均衡到相对平均的状态。

首先要做的是将直方图归一化，即将原本的纵轴归一为百分比小数的形式。

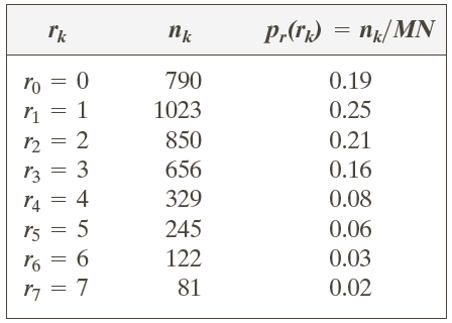
第一列的rk为横轴，第二列nk为原直方图的纵轴，第三列pr为归一化后的纵轴。

接着通过公式

S_k=L\cdot \sum^k_{j=0}p_r(r_j),k=0,1,2...L-1

计算出 $S_k$ ，通俗点说，其实就是从pr(r0)累加到pr(rk)，然后乘上灰度级数，接着执行一次四舍五入取整。

S0 = 1.33 → 1 ； S4 = 6.23 → 6

S1 = 3.08 → 3 ； S5 = 6.65 → 7

S2 = 4.55 → 5 ； S6 = 6.86 → 7

S3 = 5.67 → 6 ； S7 = 7.00 → 7

得到这一组结果后，最后只需进行一次映射，将rk像素映射到Sk上，如原本横轴为0的790个像素，现在映射到横轴为1上；原本横轴分别为5、6、7的共245+122+81个像素，全部映射到横轴为7上。这样，直方图的均衡化就完成了。

算法示意见下图：

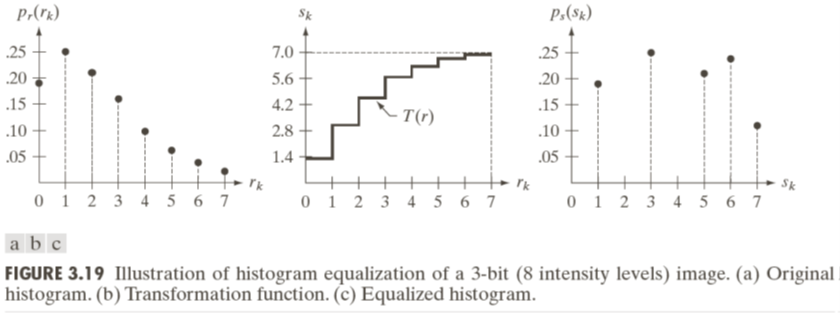
Histogram Matching

直方图匹配，目的是将一张图的直方图相似于另一张图的直方图。所用到的算法也不难，是在Histogram Equalization的基础上做了些简单的扩展。

首先，分别算出两张图的Sk，在这里我们沿用上一个例子中的S，并将引入的目标直方图的S用G来区分。

G(z0) = 0.00 → 0 ； G(z4) = 2.45 → 2

G(z1) = 0.00 → 0 ； G(z5) = 4.55 → 5

G(z2) = 0.00 → 0 ； G(z6) = 5.95 → 6

G(z3) = 1.05 → 1 ； G(z7) = 7.00 → 7

然后对于每一个Sk，找出一个最小的zq，使得G(zq)能最接近Sk。比如对于Sk=1，所能找到的zq为3；对于 Sk=3，由于G(zq)没有一个等于3，所以只能找到最接近且最小的zq，即zq为4，G(z4)=2。映射结果如下。

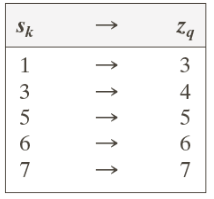
最后一步，将均衡后的原直方图纵轴完成映射，算法完整示意如下图。 注意观察Histogram Equalization算法示意的c图与下图中d图的对应关系。