数据库笔记#2：关系数据库

关系数据结构及形式化定义

关系模型 = 关系数据结构 + 关系操作集合 + 关系完整性约束
关系的三种类型：基本关系（实际存储数据的逻辑表示）、查询表（查询结果的表）、视图（虚表）

基本关系的六个性质：三列两行一分量

列是同质的
不同的列可以出自同一个域，每一列为一个属性，不同属性给予不同属性名
列的次序可以任意交换
任意两个元组的候选码不能相同
行的次序可以任意交换
分量必须取原子值，即每一分量是不可分的数据项 👈规范化的最基本条件

关系模式

关系模式的形式化定义：五元组 R ( U, D, DOM, F )
- R：关系名
- U：关系的属性名集合
- D：U中属性所来自的DOM属性向域的映象集合（？）
- F：属性间的数据依赖关系集合
- 简记为R(U)

关系操作

基本关系操作：选择、投影、并、差、笛卡尔积

关系的完整性

完整性约束：

实体完整性：若属性A是基本关系R的主属性，则A不能取空值
参照完整性：若属性F是基本关系R的外码，与它基本关系S的主码Ks相对应，则对于R中每个元组在F上的值必须为：
- 或者取空值（F的每个属性值均为空值）
- 或者等于S中某个元组的主码值

关系代数

并

$R\cup S$

两张表元组的并集

交

$R\cap S$

两张表元组的交集

差

$R-S$

两张表元组的差集

笛卡尔积

$R\times S$

将两张表的属性横向拼接，然后对元组进行全组合

象集

$Z_x$

比如有关系 R(X,Z) 如下表，那么 $Z_{x_1}$ 就是在所有元组中，X属性为 $x_1$ 的元组的Z属性的集合

选择

$\sigma_{\tiny F}(R)$

SELECT * FROM R WHERE F

投影

$\prod_{\tiny A}(R)$

SELECT A FROM R

连接

等值连接 $R\bowtie_{A=B} S$
自然连接 $R\bowtie S$ ：特殊的等值连接，去除了重复的属性列
全外连接 $R⟗S$ ：保留所有悬浮元组
左外连接 $R⟕S$ ：保留R的悬浮元组
右外连接 $R⟖S$ ：保留S的悬浮元组

用于多表查询

除

$R\div S$

对于S表中所有R中存在的属性，其值在R中某个值有对应的所有元组，算了我讲不明白，直接看例子吧：

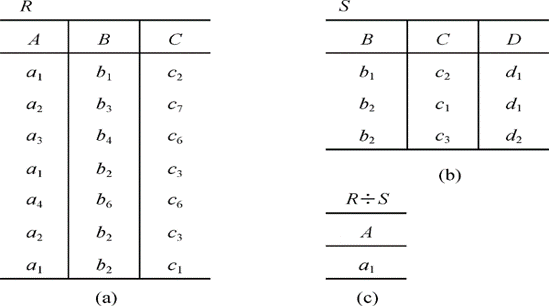
R和S共有的是B和C，S在B,C上的分量为 {(b1,c2), (b2,c1), (b2,c3)} 。此时再看R表：a1的象集为 {(b1,c2), (b2,c1), (b2,c3)} ，a2的象集为{(b3,c7), (b2,c3)} ，a3的象集为{(b4,c6)} ，a4的象集为{(b6,c6)} 。故a1即为R除S的结果。

这玩意的用法：

例1：找出选修了所有课程的学生：学生 $\div$ 所有课程

例2：找出选修了所有张三所选课的学生：学生 $\div$ 张三所选课

一般用于 “所有” 的查询